a) Xét tứ giác ABCD có 

\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)(Định lí tổng bốn góc trong một tứ giác)

mà \(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}\)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được: 

\(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\dfrac{360^0}{10}=36^0\)

Do đó: \(\widehat{A}=36^0;\widehat{B}=72^0;\widehat{C}=108^0;\widehat{D}=144^0\)

Ta có: \(\widehat{B}+\widehat{C}=180^0\)

mà hai góc này là hai góc trong cùng phía

nên AB//CD(dấu hiệu nhận biết hai đường thẳng song song)

hay ABCD là hình thang

a)  Gọi M và N lần lượt là giao điểm của AE, BF với CD.

Ta có: A D E ^ = 1 2 D ^  ngoài, D A E ^ = 1 2 A ^  ngoài.

Mà A ^  ngoài + D ^  ngoài = 1800 (do AB//CD)

⇒   A D E ^ + D A E ^ = 90 0 , tức là tam giác ADE vuông tại E.

Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.

Chứng minh tương tự, ta được F olaf trung điểm của BN.

Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM

b) Từ ý a),  EF = 1 2 ( A B + B C + C D + D A )

a: 

góc AMD=180 độ-góc MAD-góc MDA

\(=180^0-\dfrac{180^0-\widehat{BAD}}{2}-\dfrac{180^0-\widehat{ADC}}{2}\)

\(=180^0-\dfrac{1}{2}\widehat{ADC}-90^0+\dfrac{1}{2}\widehat{ADC}=90^0\)

Gọi giao của AM với DC là M'

Xét ΔDM'A có

DM là đường cao, là đường phân giác

nên ΔDM'A cân tại D

=>M là trung điểm của AM'

Gọi giao của BN với DC là N'

Ta có: \(\widehat{BNC}=180^0-\widehat{NBC}-\widehat{NCB}\)

\(=180^0-\dfrac{180^0-\widehat{ABC}}{2}-\dfrac{180^0-\widehat{BCD}}{2}\)

\(=180^0-90^0+\dfrac{1}{2}\widehat{ABC}-90^0+\dfrac{1}{2}\widehat{BCD}\)

=90 độ

Xét ΔCN'B có

CN vừa là đường cao, vừa là phân giác

nên ΔCN'B cân tại C

=>N là trug điểm của BN'

Xét hình thang ABN'M' có

M,N lần lượt là trung điểm của AM' và BN'

nen MN là đường trung bình

=>MN//CD//AB

b: MN=(AB+M'N')/2

=(AB+M'D+CD+CN')/2

mà M'D=AD và CN'=CB

nên MN=(AB+CD+AD+CB)/2

cho hình tứ giác ABCD, E là giao điểm của các đường thẳng AB và CD, F là giao điểm của các đường thẳng BC và AD. Các tia phân giác của góc E và F cắt nhau ở I. CMR:

a, Nếu góc BAD=130 độ, góc BCD= 50 độ thì IE vuông góc với IF.

b, Góc EIF bằng nửa tổng của một trong hai cặp góc đối của tứ giác ABCD

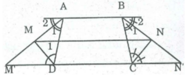
Gọi M' và N' là giao điểm của tia AM và BN với CD.

Ta có: ∠ (M') = ∠ A 2 (sole trong)

∠ A 1 =  ∠ A 2 (gt)

⇒  ∠ (M') =  ∠ A 1 nên ∆ ADM' cân tại D

* DM là phân giác của  ∠ (ADM' )

Suy ra: DM là đường trung tuyến (tính chất tam giác cân)

⇒ AM = MM'

∠ (N') =  ∠ B 1 nên  ∆ BCN' cân tại C.

* CN là phân giác của  ∠ (BCN')

Suy ra: CN là đường trung tuyến (tính chất tam giác cân)

⇒ BN = NN'

Suy ra: MN là đường trung bình của hình thang ABN'M'

⇒ MN // M'N' (tính chất đường trung hình hình thang)

Hay MN//CD

a. Đ

b.S

c.Đ

d.Đ

Ta có : KABˆ=KADˆKAB^=KAD^ ( AK là tia phân giác A^A^ )
Mà KABˆ=AKDˆKAB^=AKD^ ( so le trong )
\Rightarrow AKDˆ=KADˆAKD^=KAD^
\Rightarrow △△ ADK cân tại D
\Rightarrow AD = KD (1)

Lại có : KBAˆ=KBCˆKBA^=KBC^ ( BK là tia phân giác B^B^ )
Mà KBAˆ=BKCˆKBA^=BKC^ ( so le trong )
\Rightarrow KBCˆ=BKCˆKBC^=BKC^
\Rightarrow △△ BCK cân tại C
\Rightarrow BC = CK (2)

Cộng (1) và (2) có :
AD + BC = KD + CK
\Rightarrow AD+BCTổng hai cạnh bên=CDCạnh đáy