Vi  oA+OB+OC<GA+GB+GC+GD nen:1<2

+) Gọi AP là đường trung tuyến của \(\Delta\)ABC, giao điểm của tia AM và BC là D. Qua M kẻ đường thẳng song song với AP, nó cắt BC tại N.

Xét \(\Delta\)PDA có: M thuộc AD; N thuộc PD; MN // AP => \(\frac{MN}{AP}=\frac{DM}{DA}\Rightarrow\frac{DM}{DA}=\frac{MN}{3.GP}\) (ĐL Thales) (*)

Xét \(\Delta\)GA'P có: M thuộc GA'; N thuộc PA'; MN // GP => \(\frac{MN}{GP}=\frac{MA'}{GA'}\), thế vào (*) được

\(\frac{DM}{DA}=\frac{1}{3}.\frac{MA'}{GA'}\). Chứng minh tương tự: \(\frac{EM}{EB}=\frac{1}{3}.\frac{MB'}{GB'};\frac{FM}{FC}=\frac{1}{3}.\frac{MC'}{GC'}\)

Suy ra \(\frac{1}{3}\left(\frac{MA'}{GA'}+\frac{MB'}{GB'}+\frac{MC'}{GC'}\right)=\frac{DM}{DA}+\frac{EM}{EB}+\frac{FM}{FC}\)

\(\Rightarrow\frac{MA'}{GA'}+\frac{MB'}{GB'}+\frac{MC'}{GC'}=3\left(\frac{DM}{DA}+\frac{EM}{EB}+\frac{FM}{FC}\right)\)(1)

+) Gọi giao điểm của BM và AC là E; CM với AB là F. Qua M kẻ 2 đường thẳng song song với AB và BC, chúng cắt AC lần lượt tại H và K.

Áp dụng ĐL Thales, ta có các tỉ số: 

\(\frac{DM}{DA}=\frac{CK}{AC};\frac{FM}{FC}=\frac{AH}{AC};\frac{EM}{EB}=\frac{EH}{EA}=\frac{EK}{EC}=\frac{EH+EK}{EA+EC}=\frac{HK}{AC}\)

Cộng các tỉ số trên, ta được: \(\frac{DM}{DA}+\frac{EM}{EB}+\frac{FM}{FC}=\frac{CK+HK+AH}{AC}=\frac{AC}{AC}=1\)(2)

+) Từ (1) và (2) => \(\frac{MA'}{GA'}+\frac{MB'}{GB'}+\frac{MC'}{GC'}=3\) (đpcm).

a, https://olm.vn/hoi-dap/question/1030999.html

b,\(\frac{\sqrt{3}}{3}\)

CM PD+PE+PF=AH(đường cao)=\(\frac{\sqrt{3}AB}{2}\)

CM BD+CE+AF=\(\frac{3AB}{2}\)

D/s:\(\frac{\sqrt{3}}{3}\)

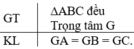
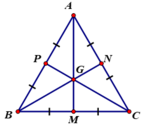
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.

Khi đó AM, BN, CP đồng quy tại trọng tâm G.

Ta có: ∆ABC đều suy ra:

+ ∆ABC cân tại A ⇒ BN = CP (theo chứng minh bài 26).

+ ∆ABC cân tại B ⇒ AM = CP (theo chứng minh bài 26).

⇒ AM = BN = CP (1)

Vì G là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:

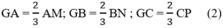
Từ (1) , (2) ⇒ GA = GB = GC.