Bài 53:
Tìm số abcd. Biết abcd + abc + ab + a = 5135
(Cách giải bằng cách sử dụng tính chất PHÉP CHIA CÓ DƯ.)

Những câu hỏi liên quan
Tìm số abcd. Biết abcd + abc + ab + a = 5135
abcd +abc+ ab+a = 5135
Sắp xếp lại các chữ số ta có:
aaaa+bbb+cc+d =
1111 x a + (111 x b+11 x c+d) = 5135
Như vậy:
5135 : 1111 = a (dư _ 111 x b+11 x c+d)
5135 : 1111 = 4 (dư 871)
a = 4 và 111 x b+11 x c+d = 871
Tương tự:
871 : 111 = 7 (dư 94)
b = 7 và 11 x c + d = 94
Tương tự:
94 : 11 = 8 (dư 6)
c = 8 và d = 6
Số cần tìm là: 4786
Đúng 0
Bình luận (0)
Bài 1:tìm các chữ số a b c d trong phép tính
abcd+abc+ab+a=4321
Bài 2:tìm số tự nhiên nhỏ nhất,biết rằng khi chia số này cho 29 thì dư 5 , còn khi chia cho 31 thì dư 28
Bài 1:
(abcd) + (abc) + (ab) + (a) = 1111.a + 111.b + 11.c + d
Vậy 1111.a + 111.b + 11.c + d = 4321
+ Nếu a < 3 => 111.b + 11.c + d > 2098 (vô lý vì b, c, d < 10)
+ Nếu a > 3 => vế trái > 4321
Vậy a = 3 => 111.b + 11.c + d = 988
+ Nếu b < 8 => 11.c + d > 210 (vô lý vì c, d < 10)
+ Nếu b > 8 => vế trái > 988
Vậy b = 8 => 11.c + d = 100
+ Nếu c < 9 => d > 11 (vô lý)
Vậy c = 9; d = 1
=> (abcd) = 3891
bài 2:
số tự nhiên A chia cho 29 dư 5 nghĩa là A = 29p + 5 ( p ∈ N ) tương tự A = 31q + 28 ( q ∈ N ) nên
31q + 28 = 29p + 5 ở đây p > q vì nếu p ≤ q ta được 31q - 29 p + 23 = 0 là vô lý vì 31q - 29 p + 23 > 0 với giả thiết p ≤ q ( 29p ≤ 29q < 31q )
vậy p > q ta có 29 ( p - q ) = 23 + 2q vì A là nhỏ nhất nên với p, q ở trên thì p - q nhỏ nhất = 1 thay lại vào ta được q = ( 29 - 23 ) : 2 = 3 vậy p = 4 thay vào ta được A = 29. 4 + 5 = 121
Thử lại 121 = 31 . 3 + 28 thỏa mãn đề bài
Đúng 0
Bình luận (0)
tìm 4 chữ số có dạng abcd, biết abcd + abc + ab + a = 4321 (ghi giùm cách giải)
Ta thấy c + c = c . Mà số duy nhất cộng nó ra chính nó là 0. Vậy c = 0
c = 0 nên b+c = b là hiển nhiên.
Ta có:a + a = d.
Vì dbc = bcc, nên d = c = b. Vậy, d và b bằng 0 => Vô lý (bạn nên xem lại đề)
Đúng 0
Bình luận (0)
Cách giải : Trong một phép chia có thương bằng 6 và số dư bằng 3 . Biết tổng của số bị chia , số chia và số dư bằng 195 . Tìm số bị chia
abcd+abc+ab+a=5135
abcd+abc+ab+a=5135
bài này dể mà !
Đúng 0
Bình luận (0)
abcd +abc+ ab+a = 5135
a x 1000+b x100+ c x 10 + d +a x100 +b x 10 +c +a x10 +b +a = 5315
a x 1111+b x 111+c x11 +d = 5315
Số dư r
Như vậy 5315 : 1111 = a ( dư : b x 111+c x11 +d )
5315 : 1111 = 4 ( dư : 871)
a = 4
Tương tự: 871 = b x 111+c x11 +d
871 : 111 = 7 ( dư : 94)
b = 7
Tương tự: 94 = c x11 +d
94 : 11 = 8 (dư : 6)
C = 8 và d = 6
Vậy so cần tìm: abcd = 4786
Đúng 0
Bình luận (0)
1)tính nhẩm bằng cách:a) Áp dụng tính chất kết hợp của phép nhân: 17.4 ;25.28b) Áp dụng tính chất phân phối của phép nhân đối với phép cộng: 13 . 12 ; 53 . 11 ; 39 . 1012) Tính nhẩm bằng cách áp dụng tính chất a(b-c) ab-ac: 8.19 ; 65 . 983) Tính tổng của số tự nhiên nhỏ nhất có 3 chữ số khác nhau và số tự nhiên lớn nhất có 3 chữ số khác nhau
Đọc tiếp
1)tính nhẩm bằng cách:
a) Áp dụng tính chất kết hợp của phép nhân: 17.4 ;25.28
b) Áp dụng tính chất phân phối của phép nhân đối với phép cộng:
13 . 12 ; 53 . 11 ; 39 . 101
2) Tính nhẩm bằng cách áp dụng tính chất a(b-c) = ab-ac:
8.19 ; 65 . 98
3) Tính tổng của số tự nhiên nhỏ nhất có 3 chữ số khác nhau và số tự nhiên lớn nhất có 3 chữ số khác nhau
1a/
17.4 = 17.(2.2) = (17.2).2 = 34.2 = 68
25.28 = 25.(4.7) = (25.4).7 = 100.7 = 700
b/
13.12 = 13.(10+2) = 13.10 + 13.2
= 130 + 26 = 156
53.11= 53.(10+1) = 53.10 + 53.1
= 530 + 53 = 583
39.101 = 39.(100+1) = 39.100 + 39.1
= 3900 + 39 = 3939
Đúng 0
Bình luận (0)
1) a/ 17.4 = 17.2.2 = 34.2 = 68
25.28 = 25.4.7 = 100.7 = 700
b/ 13.12 = 13.10 + 2 = 130 + 2 = 132
53.11 = 53.10 + 1 = 530 + 1 = 531
39.101 = 39.100 + 1 = 3900 + 1 = 3901
2) 8.19 = 8. ( 20 - 1 )
= 8.20 - 8.1
= 160 - 8 = 152
65.98 = 65. ( 100 - 2 )
= 65.100 - 65.2
= 6500 - 130 = 6370
3) - STN nhỏ nhất có 3 chữ số khác nhau là: 102
- STN lớn nhất có 3 chữ số khác nhau là: 987
Tổng của STN nhỏ nhất có 3 chữ số khác nhau và STN lớn nhất có 3 chữ số khác nhau là:
987 + 102 = 1098
Đ/S: 1098
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
bài 1: Tìm hai số tự nhiên có thương bằng 35, biết rằng nếu số bị chia tăng thêm 1056 đơn vị thì thương bằng 57. giải bằng phương pháp cấp 2.bài 2: Tìm số bị chia và số chia, biết rằng: Thương bằng 6, số dư bằng 49, tổng của số bị chia , số chia và số dư bằng 595. giải bằng phương pháp cấp 2bài 3: Một phép chia có thương bằng 4, số dư bằng 25. Tổng của số bị chia, số chia và dư bằng 210. Tìm số bị chia và số chia. giải bằng phương pháp cấp 2.Ai biết làm bài nào thì giúp mik ghi cách làm giúp mik...
Đọc tiếp
bài 1: Tìm hai số tự nhiên có thương bằng 35, biết rằng nếu số bị chia tăng thêm 1056 đơn vị thì thương bằng 57. giải bằng phương pháp cấp 2.
bài 2: Tìm số bị chia và số chia, biết rằng: Thương bằng 6, số dư bằng 49, tổng của số bị chia , số chia và số dư bằng 595. giải bằng phương pháp cấp 2
bài 3: Một phép chia có thương bằng 4, số dư bằng 25. Tổng của số bị chia, số chia và dư bằng 210. Tìm số bị chia và số chia. giải bằng phương pháp cấp 2.\
Ai biết làm bài nào thì giúp mik ghi cách làm giúp mik nhé
mik sẽ tick cho
Cảm ơn nhiều
Tìm abcd
A) ab : ( a + b ) = 5 dư 11 ([giải hai cách )
B) abcd - ab = 4629
C ) abcd + cd = 1354
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, góc ABC bằng
60
o
. Cạnh bên SA vuông góc với mặt phẳng đáy (ABCD), góc giữa SO và mặt phẳng (ABCD) bằng
45
o
. Biết khoảng cách từ điểm A đến (SCD) bằng
a
6
4
. Tính độ dài AB.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, góc ABC bằng 60 o . Cạnh bên SA vuông góc với mặt phẳng đáy (ABCD), góc giữa SO và mặt phẳng (ABCD) bằng 45 o . Biết khoảng cách từ điểm A đến (SCD) bằng a 6 4 . Tính độ dài AB.
![]()
![]()
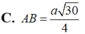
![]()