Cho hình thoi ABCD: AC=5,4cm; BD=6,8cm. Trên các cạnh AB, CD lần lượt lấy điểm M, N sao cho AMND là hình bình hành. Xác định vị trí điểm N để diện tích hình bình hành AMND=6,12 cm vuông.

Những câu hỏi liên quan
Cho hình thoi ABCD có AC = BD . Tìm tâm đường tròn ngoại tiếp hình thoi ABCD ?
A. Điểm A.
B. Giao điểm của AC và BD
C. Không có đường tròn ngoại tiếp tứ giác ABCD.
D. Trung điểm cạnh AB.
Đáp án B
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
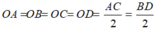
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.
Đúng 0
Bình luận (0)
cho hinh thoi ABCD biết ac=12cm:bc=1/2 ac tính diện tích hình thoi abcd và diện tích phần hình tam giác ocd
cho hình thoi ABCD . Biết AC = 24 cm,BD = 5/6 AC.tính diện tích hình thoi ABCD?
Độ dài đường chéo BD là : 24 x 5/6 = 20 { cm } ; Diện tích hình thoi ABCD là 24 x 20 : 2 = 240 { cm vuông }
Đúng 0
Bình luận (0)
Cho hình thoi ABCD. Biết AC = 60cm và độ dài đường BD bằng độ dài2/3 đường chéo AC. Tính diện tích hình thoi ABCD.
Cho hình thoi ABCD có AC=8cm, BD=6cm. Tính chu vi hình thoi ABCD
Gọi \(O\) là giao điểm của \(AC\)và \(BD\).
Theo đề ta có: \(\hept{\begin{cases}AC=8cm\\BD=6cm\end{cases}}\)
Theo tính chất của hình thoi ta có: \(\hept{\begin{cases}AO=OC=4cm\\BO=OD=3cm\end{cases}}\)
Áp dụng định lí Pitago trong \(\Delta AOB\) có:
\(AB^2=AO^2+OB^2\)
\(\Rightarrow AB=\sqrt{AO^2+OB^2}=\sqrt{4^2+6^2}\)
\(\Rightarrow AB=5cm\)
\(\Rightarrow S_{ABCD}=4AB=4.5=20cm\)
Vậy ...............
Cho hình thang ABCD có đáy AB = 1/3 CD. Đường cao AH = 3/4 AB. Tính diện tích hình thang ABCD? Biết AB = 5,4cm.
đáy lớn DC của hình thang ABCD là:
5.4 * 3 =16.2 (cm)
đường cao AH của hình thang ABCD là:
5.4 : 4 * 3 =4.05 (cm)
diện tích hình thang ABCDlà:
(16.2 + 5.4) * 4.05 : 2 =43.74(cm2)
đáp số 43.72cm2
Cho hình thoi ABCD .Biết AC = 24 cm Và độ dài đường chéo BD bằng 2/3 độ dài đường chéo AC . Tính diện tích hình thoi ABCD.
Cho hình thoi ABCD có AC=10cm , BC=24cm.
a.Tính chu vi của hình thoi ABCD
b.Tính độ dài đường cao của hình thoi
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết OA 12cm, diện tích hình thoi ABCD là
168
c
m
2
. Cạnh của hình thoi là: A.
190
(cm) B.
180
(cm) C.
193
(cm) D.
195
(cm)
Đọc tiếp
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết OA = 12cm, diện tích hình thoi ABCD là 168 c m 2 . Cạnh của hình thoi là:
A. 190 (cm)
B. 180 (cm)
C. 193 (cm)
D. 195 (cm)
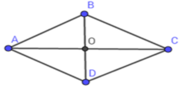
Ta có: AC = 2AO = 2.12 = 24cm
SABCD = 1 2 BD.AC
=> BD = 2 S A B C D A C = 2.168 24 =14(cm)
=> BO = 1 2 BD = 1 2 .14 = 7(cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB = A O 2 + B O 2 = 12 2 + 7 2 = 193 (cm)
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)





















