Đáp án B
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
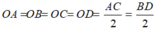
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.
Đáp án B
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
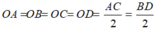
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.
Cho hình thoi ABCD. Đường trung trực của cạnh AB cắt BD tại E và cắt AC tại F. Chứng minh E, F lần lượt là tâm của đường tròn ngoại tiếp các tam giác ABC và ABD
Cho tứ giác ABCD nội tiếp (O). Gọi E là giao điểm của AB, CD. F là giao điểm của AC và BD. Đường tròn ngoại tiếp tam giác BDE cắt đường tròn ngoại tiếp tam giác FDC tại điểm K khác D. Tiếp tuyến của O tại BC cắt nhau tại M
a) CM tứ giác BKCM nội tiếp.
b) CM E,M,F thẳng hàng
Cho tứ giác ABCD nội tiếp đường tròn tâm O (AB>CD). GỌi giao điểm của AC và BD là I. Đường tròn ngoại tiếp tam giác ADI cắt AB và CD lần lượt tại E và F, EF cắt AC và BD tại M, N.
a, Chứng minh IE = IF
b, Chứng minh EF//BC và tứ giác AMND nội tiếp
c, Gọi K là tâm đường tròn ngoại tiếp tam giác ADI.
Chứng minh rằng KI vuông góc với BC
(Mình cần làm giúp phần (c) thôi ạ, cảm ơn)
Cho hình thoi ABCD. Đường trung trực của cạch AB cắt BD tại E và cắt AC tại F. Chứng minh E,F lần lượt là tâm của đường tròn ngoại tiếp các tam giác ABC và ABD
Cho hình thoi ABCD. Đường trung trực của BC cắt AC tại M và cắt BD tại N. CMR: M và N lần lượt là tâm của đường tròn ngoại tiếp các tam giác BDC và ABC.
Cho hình thoi ABCD có B= 60 độ. 1 đường thẳng qua D không cắt hình thoi nhưng cắt các đường thẳng AB và BC lần lượt tại E và F. Gọi M giao điểm AF, CE. Chứng minh AD tiếp xúc với đường tròn ngoại tiếp tam giác MDF.
cho đường tròn tâm O bán kính R có 2 đường kính AC và BD vuông góc với nhau. Gọi M là trung điểm OB. Tia AM cắt đt O ở E
A) tứ giác ABCD là hình gì? S tứ giác ABCD theo R ?
B) Cm OMEC nội tiếp và tính diện tích hình tròn ngoại tiếp tứ giác OMEC theo R
C) CM AM.AE=2 \(R^{2}\)
Cho hình thoi ABCD, \(\widehat{A}=90^0\), O là giao điểm hai đường chéo, vẽ OF vuông góc với AB (F\(\in\)AB).
a) Chứng minh đường tròn tâm O, bán kính OF tiếp xúc với bốn cạnh của hình thoi ABCD.
b) Đường tròn ngoại tiếp tam giác ABD cắt AC tại điểm thứ hai K. Chứng minh K là trực tâm của tam giác BCD.
c) Cho biết \(\widehat{BAD}=60^0\), cạnh AB=a
i. Tính diện tích hình thoi ABCD theo a
ii. Chứng minh rằng \(\frac{AO}{OK}=\frac{ÃC}{CK}\)
Từ một điểm A ở ngoài đường tròn tâm O kẻ hai tiếp tuyến AB, AC với đường tròn này.
1) Chứng minh tứ giác ABOC nội tiếp đường tròn. Xác định tâm của đường tròn ngoại tiếp tứ giác ABOC
2) Gọi điểm D là trung điểm của AC, đoạn thẳng BD cắt đường tròn tâm O tại điểm E, AE cắt đường tròn tâm O tại điểm F Chứng minh AB2 = AE.AF
3) Gọi H là giao điểm của AO và BC. Chứng minh góc DHC = góc DEC