Trong 1 phòng học có 7 dãy ghế , mỗi dãy ghế có 10 chỗ ngồi . Một nhóm học sinh gồm 50 người đến học 2 lớp buổi sáng và buổi chiều . Chứng tỏ rằng tìm được 2 người cả sáng và chiều ngồi cùng 1 dãy.

Những câu hỏi liên quan
Trong một buổi liên hoan, một lớp học mời 15 người khách tới dự. Vì lớp đã có 40 học sinh lên phải kể thêm 1 dãy ghế nữa và mỗi dayc phải ngồi thêm một người thì mới đủ chỗ. Biết mỗi dãy ghế đều có số người ngồi như nhau và ngồi khomg quá 5 người. Hỏi lớp học lúc đầu có bao nhêu dãy ghế?
Trong buổi tổng kết thi đua lớp 9 có mời 15 bạn lớp khác đến dự. vì lớp 9A có 40 học sinh nên phải kê thêm một dãy ghế nữa và mỗi dãy ghế ngồi thêm một học sinh nữa mới đủ chỗ ngồi .hỏi lớp 9A lúc đầu còn mấy dãy ghế? biết rằng mỗi dãy có số học sinh ngồi như nhau và không quá 5 học sinh
Trong buổi họp phụ huynh học sinh cuối năm của trường A, khối lớp 8 có 150 phụ huynh đến dự họp, biết rằng phòng họp ban đầu có 100 chỗ ngồi. Để chuẩn bị cho cuộc họp, người ta phải kê thêm 3 dãy ghế và mỗi dãy kê thêm 2 ghế (số lượng ghế trong mỗi dãy ghế bằng nhau). Hỏi phòng họp lúc đầu có mấy ghế, biết rằng khi phụ huynh ngồi vào họp thì còn dư 6 ghế?
Trong buổi họp phụ huynh học sinh cuối năm của trường A, khối lớp 8 có 150 phụ huynh đến dự họp, biết rằng phòng họp ban đầu có 100 chỗ. Để chuẩn bị cho cuộc họp, người ta phải kê thêm 3 dãy ghế và mỗi dãy ghế kê thêm 2 ghế (số lượng ghế trong mỗi dãy ghế bằng nhau). Hỏi phòng họp lúc đầu có mấy dãy ghế, biết rằng khi phụ huynh ngồi vào họp thì còn 6 ghế?
Trong 1 rạp hát có 7 dãy ghế.Mỗi dãy có 10 chỗ ngồi,1 nhóm học sinh đi xem xuất sáng và xuất chiều.C/m tìm được 2 học sinh xuất sáng và xuất chiều chung 1 dãy
Trong một phòng họp có 70 người dự học được sắp xếp ngồi đều trên các dãy ghế. Nếu bớt đi 2 dãy ghế thì mỗi dãy ghế còn lại phải xếp thêm 4 người mới đủ chỗ ngồi. Hỏi lúc đầu phòng họp có mấy dãy ghế và mỗi dãy ghế được xếp bao nhiêu người?
Câu hỏi tương tự nha bạn
Đúng 0
Bình luận (0)
Gọi số dãy ghế ban đầu là a [a>0 ,a thuộc N]
=>Số người trên mỗi dãy ghế là : \(\frac{70}{a}\)
Khi bớt đi 2 dãy ghế => Số dãy ghế còn lại là : a-2
Số người trên mỗi dãy ghế lúc đó là : \(\frac{70}{a-2}\)
Theo bài ra ta có : \(\frac{70}{a}+4=\frac{70}{a-2}\)
=> 70[a-2]+4a[a-2]=70a =>35[a-2]+2a[a-2]=35a
=> 35a-70+2a\(^2\)-4a=35a
=> 2a\(^2\)-4a-70=0
=> \(a^2-2a-35=0=>a^2-2a+1-36=0=>\left[a-1^2\right]=36=6^2\). Có 2 trường hợp
Trường hợp 1 : a-1 = -6 => a = - 5 [loại]
Trường hợp 2 : a - 1 = 6 => a = 7
Còn đây bạn làm nốt tiếp
Vậy phòng họp lúc đầu có 7 dãy ghế và 10 người
Đúng 1
Bình luận (0)
Gọi x là số ghế lúc đầu \(\left(x\inℤ;x>2\right)\)
Ta có phương trình \(\frac{70}{x-2}-\frac{70}{x}=4\)
Giải phương trình được x = 7 ; x = -5
Chỉ có x = 7 thỏa mãn điều kiện đề bài
Vậy lúc đầu phòng họp có 7 dãy ghế và mỗi dãy có 10 người
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Có 2 dãy ghế đối diện nhau, mỗi dãy có 6 ghế. Xếp ngẫu nhiên 12 học sinh gồm 6 nam và 6 nữ ngồi vào 2 dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với 1 học sinh nữ và không có 2 học sinh cùng giới ngồi cạnh nhau bằng. A.
11
462
B.
1
462
C.
17
462
D.
7
462
Đọc tiếp
Có 2 dãy ghế đối diện nhau, mỗi dãy có 6 ghế. Xếp ngẫu nhiên 12 học sinh gồm 6 nam và 6 nữ ngồi vào 2 dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với 1 học sinh nữ và không có 2 học sinh cùng giới ngồi cạnh nhau bằng.
A. 11 462
B. 1 462
C. 17 462
D. 7 462
Chọn B.
Phương pháp: Sử dụng hoán vị và quy tắc nhân.
Cách giải: Xếp 12 học sinh vào 12 ghế có 12! cách xếp.
Đánh số ghế như sau:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Chọn giới tính nam hoặc nữ có 2 cách.
Xếp nam hoặc nữ ngồi vào các ghế 1, 3, 5, 8, 10,12 có 6!= 720 cách.
Xếp các bạn giới tính còn lại vào 6 ghế còn lại có 6!= 720cách.
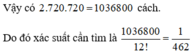
Đúng 0
Bình luận (0)
Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 2 học sinh lớp A, 2 học sinh lớp B và 2 học sinh lớp C ngồi vào dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để không có học sinh lớp C nào ngồi cạnh nhau bằng A.
2
3
B.
1
3
C.
5
6
D.
1
5
Đọc tiếp
Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 2 học sinh lớp A, 2 học sinh lớp B và 2 học sinh lớp C ngồi vào dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để không có học sinh lớp C nào ngồi cạnh nhau bằng
A. 2 3
B. 1 3
C. 5 6
D. 1 5
Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 2 học sinh lớp A, 2 học sinh lớp B và 2 học sinh lớp C ngồi vào dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để không có học sinh lớp C nào ngồi cạnh nhau bằng
Đọc tiếp
Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 2 học sinh lớp A, 2 học sinh lớp B và 2 học sinh lớp C ngồi vào dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để không có học sinh lớp C nào ngồi cạnh nhau bằng
![]()
![]()
![]()
![]()
















