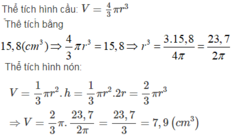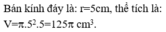Tính thể tích hình nón có chu vi đáy là 31,4 ( cm ) và chiều cao là 12 ( cm )

Những câu hỏi liên quan
Tính thể tích hình nón, biết chiều cao hình nón là 5cm và chu vi mặt đáy bằng chu vi hình vuông có diện tích 9.8596 cm2
Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính:Thể tích hình nón, biết thể tích hình cầu là 15,8
c
m
3
Đọc tiếp
Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính:
Thể tích hình nón, biết thể tích hình cầu là 15,8 c m 3
Cho một hình nón có bán kính đường tròn đáy là r (cm), chiều cao 2r (cm) và một hình cầu có bán kính r (cm). Hãy tính:a, Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06
c
m
2
b, Thể tích của hình nón, biết thể tích của hình cầu là 15,8
c
m
3
Đọc tiếp
Cho một hình nón có bán kính đường tròn đáy là r (cm), chiều cao 2r (cm) và một hình cầu có bán kính r (cm). Hãy tính:
a, Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06 c m 2
b, Thể tích của hình nón, biết thể tích của hình cầu là 15,8 c m 3
a, Tính được r = 1,44cm Þ Smc = 4p r 2 = 26,03 c m 2
b, Ta có V c = 4 3 πR 2 = 15 , 8 cm 3 => R = 1,56cm
=> V h n = 1 3 πR 2 h ≈ 2 , 53 πcm 3
Đúng 0
Bình luận (0)
Từ một khúc gỗ hình trụ cao 15 cm, người ta tiện thành một khối gỗ hình nón với chiều cao giữ nguyên từ khúc gỗ ban đầu và đáy nón chính là đáy khúc gỗ hình trụ. Biết phần
gỗ bỏ đi có thể tích là 640r(cm). Tính thể tích khối gỗ hình nón đã tiện được.
Lời giải:
Gọi bán kính đáy khúc gỗ là $r$ (cm) thì:
Thể tích khúc gỗ:
$\pi r^2h=15\pi r^2$ (cm khối)
Thể tích hình nón:
$\frac{1}{3}\pi r^2h=5\pi r^2$ (cm khối)
Thể tích phần bỏ đi:
$15\pi r^2-5\pi r^2=640r$ (cm khối)
$10\pi r^2=640r$
$10\pi r=640$
$r=\frac{64}{\pi}$ (cm)
Thể tích khối nón: $5\pi r^2=5\pi.\frac{64^2}{\pi ^2}=\frac{20480}{\pi}$ (cm khối)
Đúng 1
Bình luận (0)
Nghe đề bài có vẻ sai sai. Nếu đề là $640\pi$ (cm khối) thì bạn cũng làm tương tự, $r=8$ (cm)
Đúng 1
Bình luận (0)
Tổng độ dài một cạnh đáy và chiều cao tư ứng là 4 dm 8cm , chiều cao hơn cạnh đáy 12 cm A tính diện tích hình bình hành đó B một hình chữ nhật có diện tích bằng diện tích hình bình hành trên chiều dài là 36 cm. Tính chu vi hình chữ nhật đó
đổi : 4dm8cm = 48 cm
đáy hình bình hành là : ( 48 - 12 ) : 2 = 18 ( cm )
chiều cao hình bình hành là : 48 - 18 = 30 ( cm )
a)diện tích hình bình hành là : 18 x 30 = 540 ( cm2 )
b) chiều rộng hình chữ nhật là : 540 : 36 = 15 ( cm )
chu vi hình chữ nhật là : ( 15 + 36 ) x 2 = 102 ( cm )
đáp số : a)540 cm2 ; b) 102 cm
/HT\
Một hình trụ có chu vi đáy bằng 10p cm và có chiều cao là 5cm. Tính thể tích V của hình trụ? A.
V
125
3
c
m
3
B. V50p
c
m
3
C. V500p
c
m
3
D. V125p
c
m
3
Đọc tiếp
Một hình trụ có chu vi đáy bằng 10p cm và có chiều cao là 5cm. Tính thể tích V của hình trụ?
A. V = 125 3 c m 3
B. V=50p c m 3
C. V=500p c m 3
D. V=125p c m 3
Một hình lăng trụ có đáy là hình thoi cới các đường chéo của đây bằng 24cm và 10 cm chu vi đáy là 52 cm diện tích toàn phần của hình lăng trụ là 1020 cm vuông tính chiều cao và thể tích của hình lăng trụ đó
Gọi đường chéo của hình thoi là d và chu vi đáy là p.
Ta có hệ phương trình sau:
d + d = 24cm (vì đường chéo của hình thoi bằng 24cm)
p = 52cm (vì chu vi đáy của hình thoi bằng 52cm)
Từ đó, ta có:
2d = 24cm
d = 12cm
Vậy đường chéo của hình thoi là 12cm.
Để tính chiều cao của hình lăng trụ, ta sử dụng định lý Pytago:
Chiều cao của hình lăng trụ = căn bậc hai của (d^2 - (cạnh đáy/2)^2)
= căn bậc hai của (12^2 - (10/2)^2)
= căn bậc hai của (144 - 25)
= căn bậc hai của 119
≈ 10.92cm
Vậy chiều cao của hình lăng trụ là khoảng 10.92cm.
Để tính thể tích của hình lăng trụ, ta sử dụng công thức:
Thể tích = diện tích đáy x chiều cao
= (diện tích hình thoi x 2) x chiều cao
= (cạnh đáy x cạnh đáy x sin(góc giữa hai đường chéo) x 2) x chiều cao
= (10cm x 10cm x sin(90°) x 2) x 10.92cm
= (100cm^2 x 1 x 2) x 10.92cm
= 2184cm^3
Vậy thể tích của hình lăng trụ là 2184cm^3
Đúng 0
Bình luận (0)
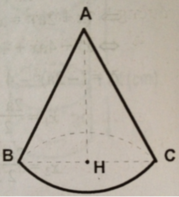
Một hình nón có chiều cao là 12 cm, bán kính đường tròn đáy là 5 cm. Tính diện tích xung quanh của hình nón.
GIÚPPPPPPPPPPPPPPPPPPPPPPP
Theo pytago ta có
\(l^2=h^2+r^2=12^2+5^2=169=13^2\)
\(\Rightarrow l=13\)
\(S_{xq}=\Pi.r.l=3,14.5.13=204,1cm^2\)
Đúng 1
Bình luận (0)
Ta có: \(l^2=h^2+r^2\left(pytago\right)\)
=> \(l^2=12^2+5^2=169\)
=> l = 13 (cm)
Diện tích xung quanh hình nón là:
\(S_{xp}=\pi rl\approx3,14.5.13=204,1\left(cm^2\right)\)
KL: Diện tích xung quanh hình nón là 204,1 cm2
Đúng 0
Bình luận (0)
Hãy tính:
a) Diện tích xung quanh của một hình trụ có chu vi hình tròn đáy là 13 cm và chiều cao là 3 cm.
b) Thể tích của hình trụ có bán kính đường tròn đáy là 5 mm và chiểu cao là 8 mm.
Giải:
a) Ta có: C = 13m, h = 3cm
Diện tích xung quanh của hình trụ là: Sxp = 2 πr.h = C.h = 13.3 = 39 cm2
b) Ta có r = 5 mm , h = 8mm
Thể tích của hình trụ là:
V = πr2h = π.52.8 = 200π ≈ 628 mm3
Đúng 0
Bình luận (0)