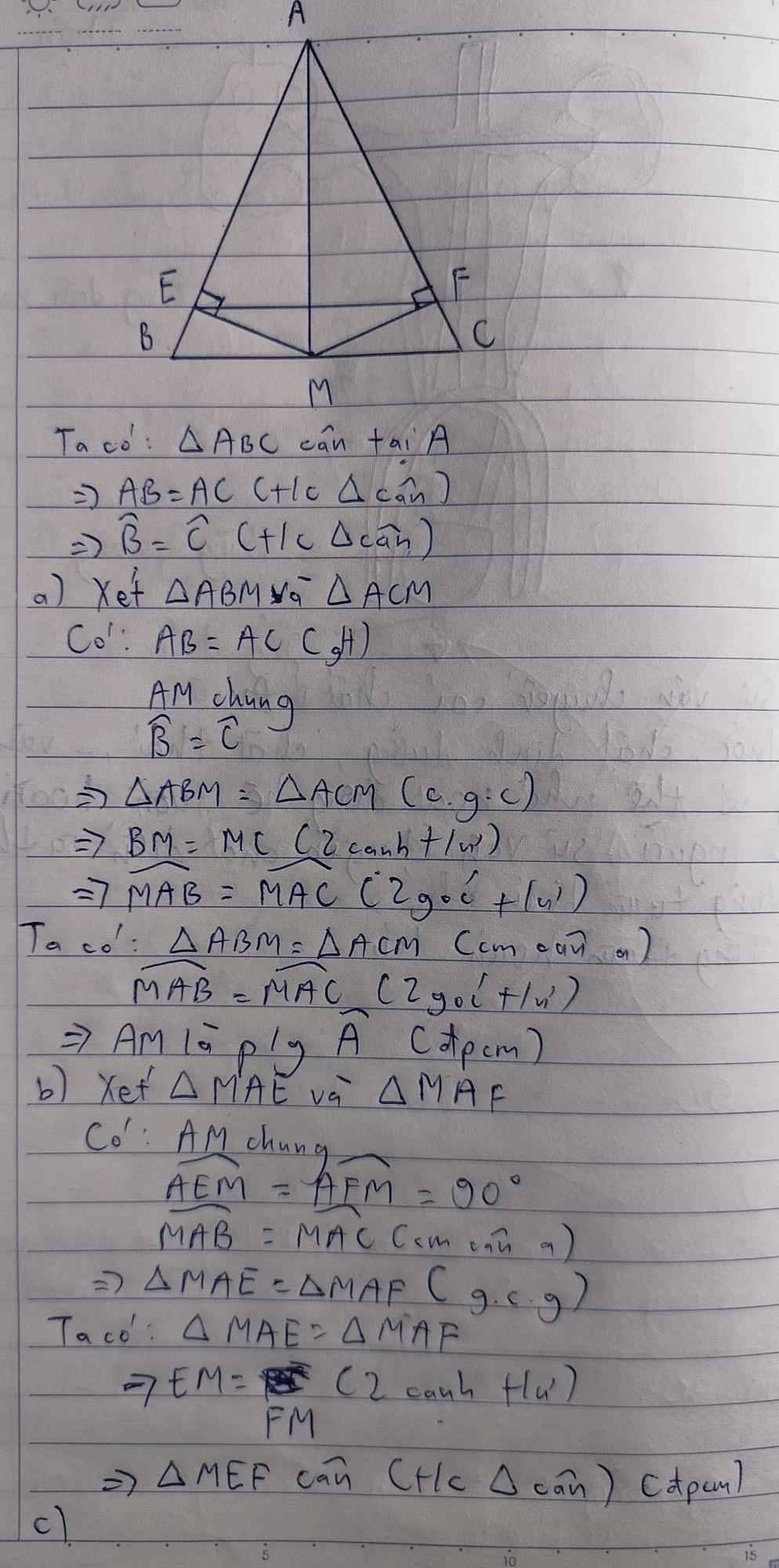Những câu hỏi liên quan
Cho tam giác ABC cân tại a đường vuông góc với 2 cạnh bên tại b và c cắt nhau tại m Chứng minh tam giác ABM = tam giác ACM Chứng minh AM là phân giác của góc BAC
a) Xét ΔABM vuông tại B và ΔACM vuông tại M có
AM chung
AB=AC(ΔABC cân tại A)
Do đó: ΔABM=ΔACM(cạnh huyền-cạnh góc vuông)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A có A^=20.Điểm M nằm ở trong tam giác sao cho tam giác MBC đều .chứng minh :
a,Tia AM là phân giác của góc BAC
b,góc ABM=góc ACM=góc BAC
Helppppppppppppppppppppppppppppppppppppppppppp me
Đúng 0
Bình luận (0)
câu a: xét \(\Delta AMB\) và \(\Delta AMC\)có :
AB=AC(gt)
MB=MC(tam giác MBC cân)
AM là cạnh chung
\(\Rightarrow\Delta AMB=\Delta AMC\)(C.C.C)
\(\Rightarrow\)\(\widehat{BAM}=\widehat{CAM}\)
Vậy AM là tia phân giác\(\widehat{BAC}\)
B)
góc ABM= góc ACM= \(\frac{180º-20º}{2}-60º=20º\)
Vậy \(\widehat{ABM}=\widehat{ACM}=\widehat{BAC}\)
Đúng 0
Bình luận (0)
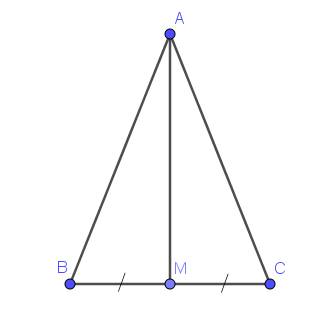
Bài 17: Cho tam giác ABC cân tại A. Gọi M là trung điểm BC.
a, Chứng minh \(\Delta\) ABM =\(\Delta\) ACM
b, Chứng minh AM là phân giác góc BAC và AM vuông góc BC.
c, Lấy E bất kì trên đoạn AM. Chứng minh tam giác EBC cân.
Lời giải:
a.
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.
Đúng 2
Bình luận (0)
Cho tam giác ABC có AB=AC.Điểm M là trung điểm của BC
a,Chứng minh tam giác ABM bằng tam giác ACM
b,Chứng minh AM vuông góc với BC
c,Chứng minh AM là tia phân giác của góc bAc
cho tam giác ABC cân tại A (A nhỏ hơn 90 độ có AM là đường trung tuyến)a) chứng minh tam giác ABM tam giác ACM và AM là tia phân giác góc Ab) từ M vẽ ME vuông góc với AB tại E; MF vuông góc với AC tại F, chứng minh tam giác MAE tam giác MAF và tam giác MEF cânc) trên tia đối của tia MA lấy điểm H sao cho MAMH, gọi M là trung điểm (H,y là giao điểm của CB và AN) chứng minh BC bằng 6 lần MIcần gấp ạ!!
Đọc tiếp
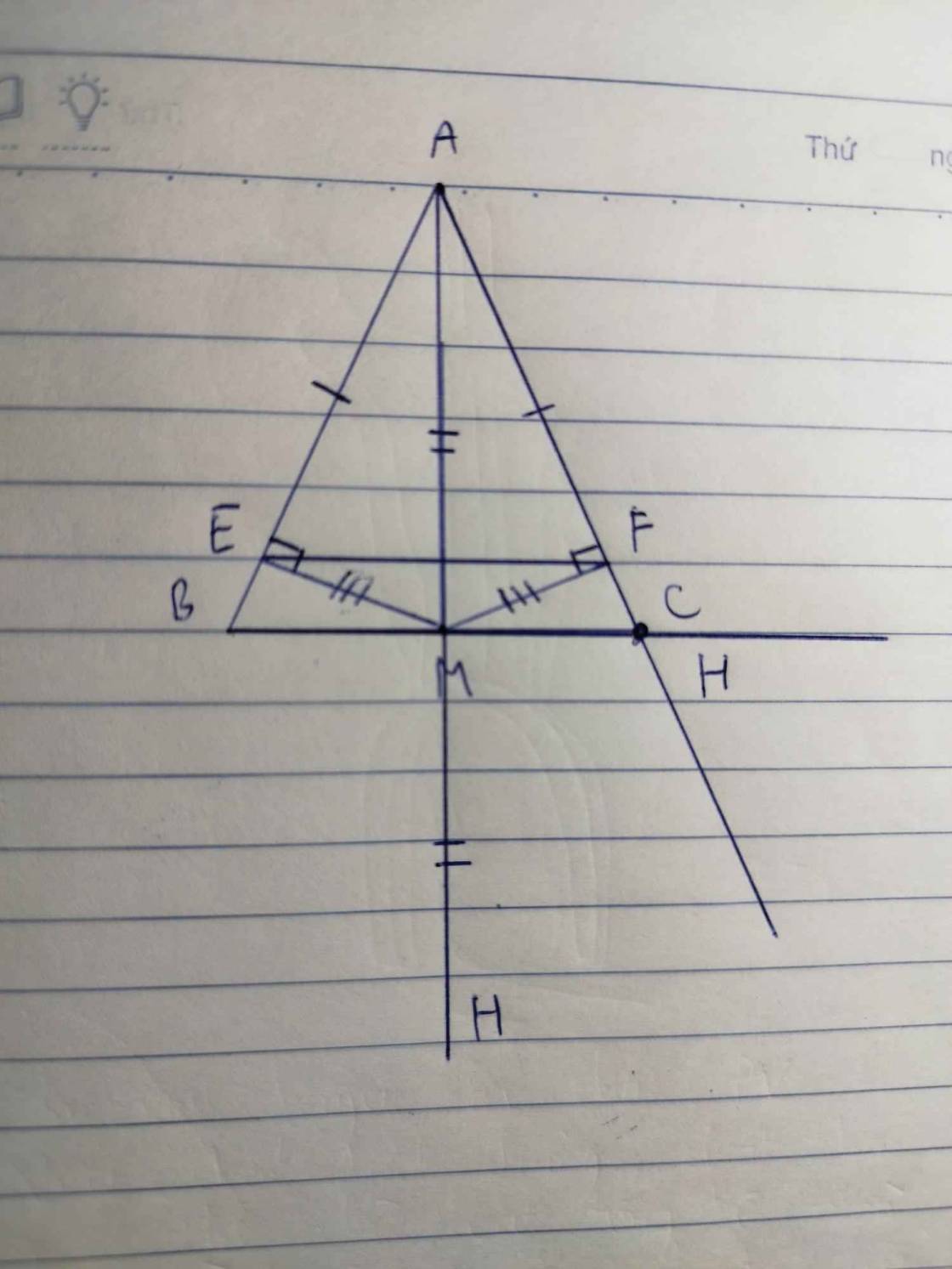
cho tam giác ABC cân tại A (A nhỏ hơn 90 độ có AM là đường trung tuyến)
a) chứng minh tam giác ABM = tam giác ACM và AM là tia phân giác góc A
b) từ M vẽ ME vuông góc với AB tại E; MF vuông góc với AC tại F, chứng minh tam giác MAE = tam giác MAF và tam giác MEF cân
c) trên tia đối của tia MA lấy điểm H sao cho MA=MH, gọi M là trung điểm (H,y là giao điểm của CB và AN) chứng minh BC bằng 6 lần MI
cần gấp ạ!!
Giúp mk bài này vs mọi người ơi!!!
Cho tam giác ABC cân tại A. Vẽ tia phân giác của góc BAC cắt cạnh BC tại M.
a) Chứng minh tam giác ABM= tam giác ACM và AM vuông góc tại BC
b) Vẽ trung tuyến BQ của tam giác ABC cắt AM tại G. Chứng minh: G là trọng tâm của tam giác ABC.
c) Cho AB= 15 cm, BC = 18cm. Tính độ dài đoạn thẳng AG
A) XÉT \(\Delta ABM\)VÀ\(\Delta ACM\)CÓ
\(AB=AC\left(GT\right)\)
\(\widehat{A_1}=\widehat{A_2}\left(GT\right)\)
AM LÀ CẠNH CHUNG
=>\(\Delta ABM\)=\(\Delta ACM\)( C-G-C)
TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ ĐƯỜNG CAO
=> AM LÀ ĐƯỜNG CAO CỦA \(\Delta ABC\)
\(\Rightarrow AM\perp BC\)
B) TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ TRUNG TUYẾN
=> AM LÀ TRUNG TUYẾN THỨ NHẤT CỦA \(\Delta ABC\)
MÀ BG LÀ ĐƯỜNG TRUNG TUYẾN THỨ HAI CỦA \(\Delta ABC\)
HAI ĐƯỜNG TRUNG TUYẾN NÀY CẮT NHAU TẠI G
\(\Rightarrow G\)LÀ TRỌNG TÂM CỦA \(\Delta ABC\)
Cho tam giác ABC có AB = AC , M là trung điểm của BC.
a ) Chứng minh : Tam giác ABM bằng tam giác ACM .
b) Chứng minh : AM là tia phân giác của góc BAC.
c ) Chứng minh : AM vuông góc với BC tại M. giúp mik vs
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Đúng 1
Bình luận (0)
\(a,\) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\) (giả thiết)
\(AM\) là cạnh chung
\(BM=CM\) (giả thiết)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
\(b,\) Vì \(\Delta ABM=\Delta ACM\) (chứng minh câu \(a\))
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\) (\(2\) góc tương ứng)
\(\Rightarrow AM\) là tia phân giác \(\widehat{BAC}\)
\(c,\) Vì \(\Delta ABC\) cân tại \(A\) (giả thiết)
Mà \(AM\) là tia phân giác \(\widehat{BAC}\) (chứng minh câu \(b\))
\(\Rightarrow AM\) là đường trung trực \(\Delta ABC\)
\(\Rightarrow AM\perp BC\) tại \(M\)
Đúng 2
Bình luận (0)
Cho tam giác ABC có AB=AC,M trung điểm BC, Chứng Minh:
a)Tam Giác ABM= Tam Giác ACM
b)AM phân Giác Góc BAC
cho tam giác ABC có AB=AC và BC<AB,gọi M là trung điểm của BC
a)c/m: tam giác ABM=tam giác ACM và AM là tia phân giác của góc BAC
b)trên cạnh AB lấy điểm D sao cho CB=CD.Kẻ tia phân giác của góc BCD,tia này cắt cạnh BD tại N . CHỨNG MINH: CN vuông góc BD
c)trên tia đối của tia CA lấy điểm E sao cho AD=CE, chứng minh: BE-CE=2BN