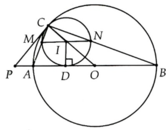
Cho đường tròn (O), đường kính AB và một điểm C \(\in\)(O). Một đường tròn (I) tiếp xúc với (O) tại C và tiếp xúc với đường kính AB tại D. AC cắt (I) tại M; BC cắt (I) tại N. Chứng minh:
a) MN là đường kính của ( I )
b) ID \(⊥\)MN
c) CD đi qua một điểm cố định khi (I) thay đổi