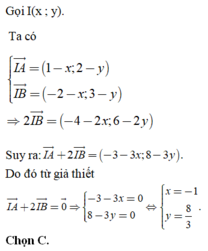Trong hệ tọa độ Oxy, cho ba điểm A(1; 3); B(-1; 2); C(-2; 1). Tìm tọa độ của vectơ A B → − A C → .
A. (-5; -3)
B. (1; 1)
C. (-1; 2)
D. (-1; 1)
A B → = − 2 ; − 1 A C → = − 3 ; − 2 ⇒ A B → − A C → = − 2 − − 3 ; − 1 − − 2 = 1 ; 1 .
Đáp án B
Trong hệ tọa độ Oxy, cho hai điểm A(1; 2) ; B(- 2; 3). Tìm tọa độ đỉểm I sao cho I A → + 2 I B → = 0 → .
A. I 1 ; 2 .
B. I 1 ; 2 5 .
C. I − 1 ; 8 3 .
D. I 2 ; − 2 .
1.Trong mặt phẳng hệ tọa độ Oxy, viết phương trình đường thẳng Δ qua M(1,2) cắt Ox tại A, cắt Oy tại B sao cho OA+OB =12 2.Cho 3 điểm A(2,0), B(3,4), C(1,1), Viết phương trình đưởng thẳng qua C cách đều hai điểm A, B 3.Trong hệ tọa độ Oxy cho tam giác ABC có BC= x+y=9=0, đường cao B, C lần lượt là: d1: x+2y-13=0, d2:7x=5y-49=0. Tìm tọa độ điểm A
trong mặt phẳng hệ tọa độ Oxy cho hai điểm A(3;-1) ; B(1;1) . Tìm tọa độ điểm E biết điểm E thuộc trục tung và 3 điểm A , B , E thẳng hàng .
Trong mp với hệ tọa đô Oxy cho hai điểm A(1;-2), B(-4;5). Tìm tọa độ điểm M trên trục Oy sao cho 3 điểm M,A,B thẳng hàng
Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3); B (3; 4) Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng.
A. M (1 ; 0)
B. M(4; 0)
C. M − 5 3 ; − 1 3 .
D. M 17 7 ; 0 .
Trong hệ tọa độ Oxy, cho hai điểm A(2 ; -3) ; B ( 4 ; 7). Tìm tọa độ trung điểm I của đoạn thẳng AB
A. I( 6 ; 4)
B. I (2 ; 10)
C. I (3 ; 2)
D. I( 8; -21)
x I = 2 + 4 2 = 3 y I = − 3 + 7 2 = 2 ⇒ I 3 ; 2 .
Đáp án C
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3) ; B(4; 7). Tìm tọa độ trung điểm I của đoạn thẳng AB?
A. (6; 4)
B.(2; 10)
C. (3; 2)
D.( 8; -21)
x I = 2 + 4 2 = 3 y I = − 3 + 7 2 = 2 ⇒ I 3 ; 2 .
Đáp án C
trong hệ tọa độ oxy cho 3 điểm a (1;3), B (4;0), C (2; -5). Tìm tọa độ điểm M thỏa mãn hệ thức vecto MA + vecto MB - 3 vecto MC = vecto 0 ?
trong hệ tọa độ oxy cho 3 điểm a (1;3), B (4;0), C (2; -5). Tìm tọa độ điểm M thỏa mãn hệ thức vecto MA + vecto MB - 3 vecto MC = vecto 0 ?
Gọi tọa độ điểm \(M\) là \(M\left(x;y\right).\)
\(\overrightarrow{MA}=\left(1-x;3-y\right);\overrightarrow{MB}=\left(4-x;-y\right);\overrightarrow{MC}=\left(2-x;-5-y\right).\)
Ta có: \(\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=\overrightarrow{0}.\)
\(\left\{{}\begin{matrix}1-x+4-x-3\left(2-x\right)=0.\\3-y-y-3\left(-5-y\right)=0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-2x+5-6+3x=0.\\3-2y+15+3y=0.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=0.\\y+18=0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1.\\y=-18.\end{matrix}\right.\) \(\Rightarrow M\left(1;-18\right).\)
