Xác định hàm số bậc nhất biết đồ thị hàm số.
đi qua M có tọa độ(1,-1), N(3,1).
Cắt đường thẳng y=x+1 tại 1 điểm có hoành độ bằng 4 và đi qua A(2,1)
Cho hàm số bậc nhất y=(2m-1)x+m-3. Tìm m để hàm số bậc nhất đi qua 2 điểm có tọa độ 2,5. Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ = căn 2 -1. Chứng minh rằng đồ thị hàm số luôn đi qua 1 điểm cố định với mọi m.
Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau:
a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5.
b) a = 3 và đồ thị của hàm số đi qua điểm A(2; 2)
c) Đồ thị của hàm số song song với đường thẳng y = √3 x và đi qua điểm B(1; √3 + 5 ).
a) Với a = 2 hàm số có dạng y = 2x + b.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5 khi đó tung độ bằng 0 nên:
0 = 2.1,5 + b => b = -3
Vậy hàm số là y = 2x – 3
b) Với a = 3 hàm số có dạng y = 3x + b.
Đồ thị hàm số đi qua điểm (2; 2), nên ta có:
2 = 3.2 + b => b = 2 – 6 = - 4
Vậy hàm số là y = 3x – 4
c) Đường thẳng y = ax + b song song với đường thẳng y = √3 x nên a = √3 và b ≠ 0. Khi đó hàm số có dạng y = √3 x + b
Đồ thị hàm số đi qua điểm (1; √3 + 5) nên ta có:
√3 + 5 = √3 . 1 + b => b = 5
Vậy hàm số là y = √3 x + 5
cho hàm số y = (m-1)x + m - 5
a) xác định m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3
b) xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -1
c) xác định m để đồ thị hàm số đi qua gốc tọa độ
a: Thay x=0 và y=3 vào y=(m-1)x+m-5, ta được:
\(0\cdot\left(m-1\right)+m-5=3\)
=>m-5=3
=>m=8
b: Thay x=-1 và y=0 vào y=(m-1)x+m-5, ta được:
\(-\left(m-1\right)+m-5=0\)
=>-m+1+m-5=0
=>-4=0(vô lý)
c: Thay x=0 và y=0 vào y=(m-1)x+m-5, ta được:
\(0\left(m-1\right)+m-5=0\)
=>m-5=0
=>m=5
Xác định hàm số bậc nhất y= ax+b ,biết
a, hệ số góc bằng 2 và đồ thị hàm số đi qua A( 1;2)
b,đồ thị hàm số đi qua điểm A(-2;2) và cắt đường thẳng (d) y=-2x+4 tại điểm có hoành độ bằng 3
a) Hệ số góc bằng 2
=> a=2
Đồ thị hàm số đi qua A (1; 2)
=> 2=a.1+b<=> 2=2.1+b <=> b=0
Vậy hàm số: y=2x
b)
+) Đồ thị hàm số đi qua điểm A (-2; 2)
=> 2=a. (-2)+b <=> -2a+b=2 (1)
+) Đồ thị hàm số cắt đường thẳng (d) y=-2x+4 tại điểm có hoành độ bằng 3
Gọi điểm đó là: B(3; y)
(d) qua B(3; y) => y=-2.3+4=-2
=> B(3; -2)
đồ thị hàm số qua B => -2=a.3+b <=> 3a+b=-2 (2)
Từ (1); (2) ta có:a=-4/5, b=2/5
Vậy: y=-4/5 x+2/5
a, Tìm hàm số bậc nhất biết đồ thị của nó đi qua điểm A(-1;-5) và có tung độ gốc
bằng -3.
b, Tìm m để đường thẳng y=(m-1)x+m-2 cắt nhau tại 1 điểm trên trục tung
c, Tìm m để đường thẳng y=(m-1)x+m-2 đi qua gốc tọa độ .
d,. Tìm m để đường thẳng y=(m-1)x+m-2 cắt đồ thị hàm số tìm được ở câu a tại điểm có hoành độ -6
Cho hàm số y=(2m-1)x+m-1.Xác định m để:
a)Hàm số nghịch biến trong R
b)Đồ thị hàm số cắt trục hoành tại điểm tại điểm có hoành độ -1
c)Đồ thị hàm số đi qua điểm M(1;4).Tính khoảng cách từ gốc tọa độ O đến đường thẳng đó
a: Để hàm số nghịch biến trên R thì 2m-1<0
=>2m<1
=>\(m< \dfrac{1}{2}\)
b; Thay x=-1 và y=0 vào y=(2m-1)x+m-1, ta được:
\(\left(-1\right)\left(2m-1\right)+m-1=0\)
=>-2m+1+m-1=0
=>-m=0
=>m=0
c: Thay x=1 và y=4 vào y=(2m-1)x+m-1, ta được:
\(1\left(2m-1\right)+m-1=4\)
=>2m-1+m-1=4
=>3m=6
=>m=2
Khi m=2 thì \(y=\left(2\cdot2-1\right)x+2-1=3x+1\)
=>3x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng 3x-y+1=0 là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot3+0\cdot\left(-1\right)+1\right|}{\sqrt{3^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{10}}\)
Cho hàm số y=(2m-1)x+m-1.Xác định m để
a)Hàm số nghịch biến trong R
b) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ -1
c)Đồ thị hàm số đi qua điểm M(1;4).Khi đó vẽ đồ thị hàm số.Tính khoảnh cách từ gốc tọa độ O đến đường thẳng đó.
a: Để hàm số y=(2m-1)x+m-1 nghịch biến trên R thì 2m-1<0
=>2m<1
=>\(m< \dfrac{1}{2}\)
b: Thay x=-1 và y=0 vào y=(2m-1)x+m-1, ta được:
-(2m-1)+m-1=0
=>-2m+1+m-1=0
=>-m=0
=>m=0
c: Thay x=1 và y=4 vào y=(2m-1)x+m-1, ta được:
2m-1+m-1=4
=>3m-2=4
=>3m=6
=>m=2
Khi m=2 thì \(y=\left(2\cdot2-1\right)x+2-1=3x+1\)
vẽ đồ thị:
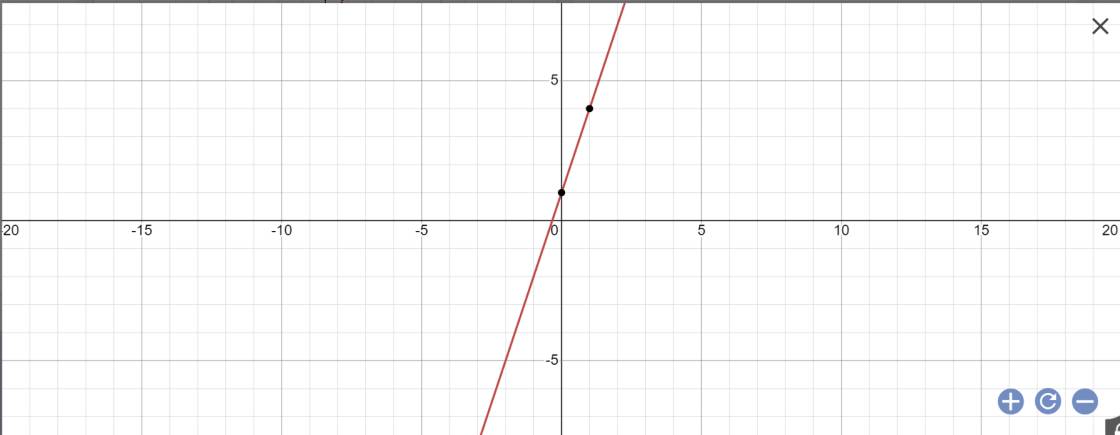
y=3x+1
=>3x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng 3x-y+1=0 là:
\(d\left(O;3x-y+1=0\right)=\dfrac{\left|0\cdot3+0\cdot\left(-1\right)+1\right|}{\sqrt{3^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{10}}\)
Bài 1. Cho hàm số y=(2m+3)x+m−1 có đồ thị là đường thẳng d . a) Xác định hàm số biết đường thẳng d đi qua điểm C(3;1). b) Xác định hàm số biết đường thẳng d cắt trục hoành tại điểm có hoành độ băng −1. c) Xác định hàm số biết đường thẳng d cắt trục tung tại điểm có tung độ bằng 3. Bài 2. Cho hàm số y=(-2m+1)x+m+3 có đồ thị là đường thẳng d . a) Xác định hàm số biết đường thẳng d có hệ số góc bằng 5. b) Xác định hàm số biết đường thẳng d song song với đường thẳng d:y=3x+7. c) Xác định hàm số biết đường thẳng d vuông góc với đường thẳng d, :y= -1/2x+5
2:
a: Hệ số góc là 5 nên -2m+1=5
=>-2m=4
=>m=-2
b: (d1)//(d)
=>-2m+1=3 và m+3<>7
=>m=-1
c: Hai đường vuông góc với nhau
=>-1/2(-2m+1)=-1
=>m^2-1/2+1=0
=>m^2+1/2=0(loại)
Bài 1:
a)Xác định hàm số bậc nhất y=ax+b biết rằng đồ thị hàm số là đường thẳng cắt trục tung tại điểm có tung độ là -3 và đi qua điểm A(1;-2)
b) Xác định tọa độ giao điểm đường thẳng vừa tìm đc với đường thẳng y=3x+5