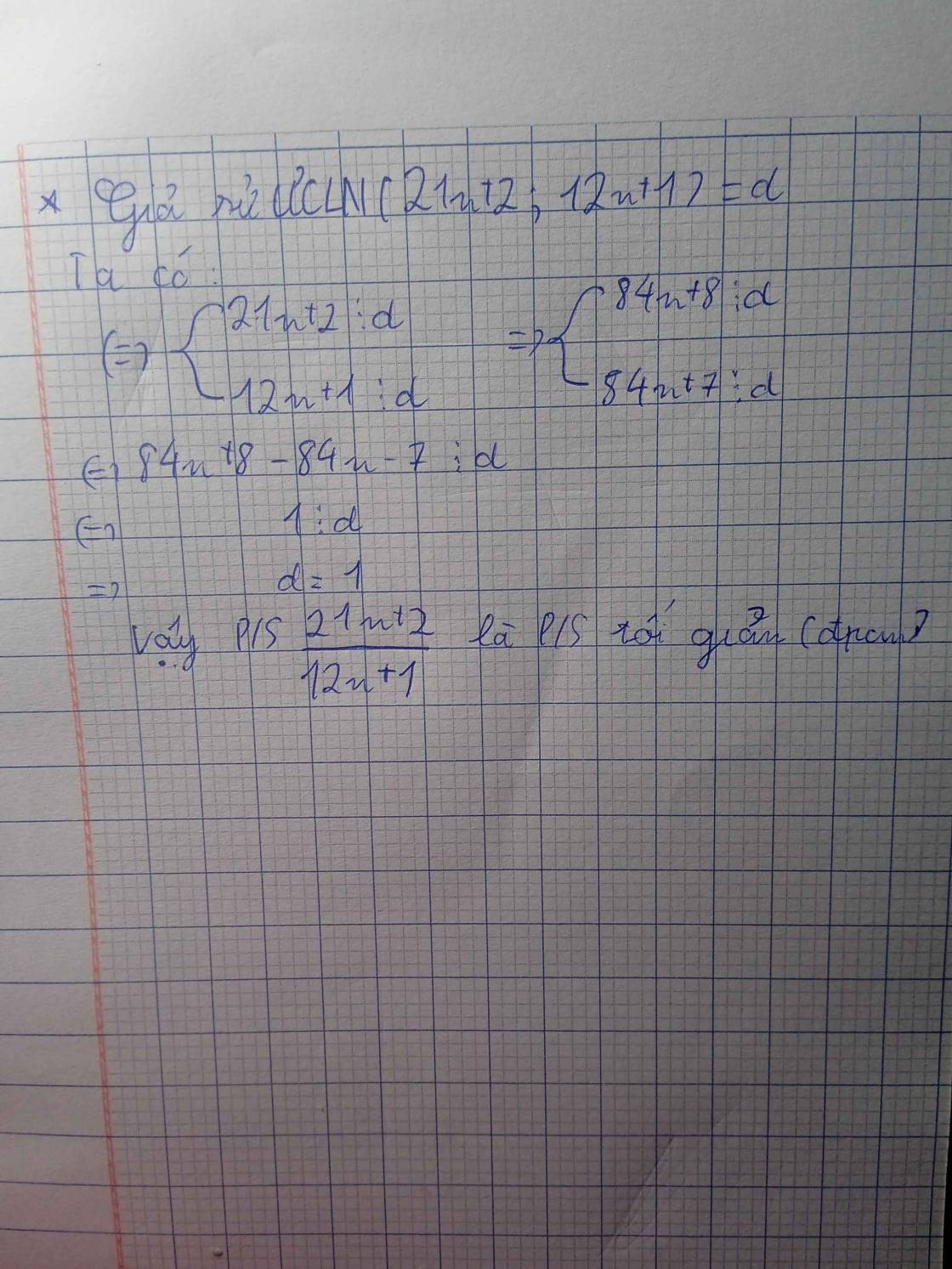Mọi người ai trả lời giúp mình với ! @_@

Sau một hồi tìm hiểu thì mình đã có lời giải r, bạn nào chưa bt thì tham khảo nhé !

Vì 12n+1 = 12n +24 - 23 = 12 (n+2) - 23

=> 12n+1 / 2 (n+2) = 12 (n+2) - 23 / 2n (n+2) = 12 (n+2) / 2n (n+2) - 23 / 2n (n+2) = 6 / n - 23 / 2n (n+2)

Ta có: 2n (n+2) chia hết cho 2

=> 2n (n+2) là số chẵn

Mà 23 là số lẻ nên phân số 23 / 2n (n+2) là phân số tối giản

=> 6 / n - 23 / 2n (n+2) là phân số tối giản

Vậy 12n+1 / 2 (n+2) là phân số tối giản

Quách Dương Hà Anh mình ch bt là bạn giải đúng hay sai nhưng nếu giải thích là số lẻ/ số chẵn là phân số tối giản thì sai nhé.

VD: 3/12 = 1/4.

Phải giải thích là 23 là số nguyên tố => 23 chỉ chia hết cho chính nó và 1.

Mà 23 và 1 là số lẻ, còn 2n(n+2) là số chẵn nên 23 không chia hết cho 2n(n+2) =>....

a/

Gọi $d=ƯCLN(n+1, 2n+3)$

$\Rightarrow n+1\vdots d; 2n+3\vdots d$

$\Rightarrow 2n+3-2(n+1)\vdots d$

$\Rightarrow 1\vdots d$

$\Rightarrow d=1$
Vậy $\frac{n+1}{2n+3}$ là phân số tối giản với mọi số tự nhiên $n$

b/

Cho $a=2, b=2$ thì phân số đã cho bằng $\frac{24}{26}$ không là phân số tối giản bạn nhé. 

Bạn xem lại đề.

  Nhớ tick cho mình nha

 Gọi UWCLN(2n+1;4n²+1) = d : (n thuộc N)

Suy ra : 2n + 1 chia hết cho d , do đó 2n(2n+1)chia hết cho d

                                                     hay 4n² + 2n chia hết cho d

Áp dụng tính chất chia hết của 1 hiệu 

  4n² + 2n - (2n + 1) chia hết cho d

Theo bài ra 4n² + 1 chia hết cho d . Áp dụng tính chất chia hết của 1 hiệu , ta được

4n² - 1 - (4n² -1) chia hết cho d

4n² - 4n² + 1 chia hết cho d

  2 chia hết cho d

Suy ra : d = {1;2}

Vì 2n + 1 và 4n² + 1 là các số lẻ nên d=1

                         Vậy 2n+1 là các số tối giản với mọi số tự nhiên n

Hướng dẫn giải:

Gọi d là ƯCLN của 12n + 1 và 30n + 2

⇒ (12n + 1)⋮ d và (30n + 2)⋮ d

⇒ [5(12n + 1) - 2(30n + 2)] ⋮ d

⇒ 1 ⋮ d, với ∀n ∈ N

⇒ d = 1 hoặc d = -1

Vậy phân thức đã cho tối giản với ∀n ∈ N 

Đặt \(d\) là \(\text{Ư}CLN\) \(\left(12n+1;30n+2\right)\)

Theo bài ra: \(12n+1⋮d\Rightarrow5.\left(12n+1\right)⋮d\left(1\right)\)

                    \(30n+2⋮d\Rightarrow2\left(30n+2\right)⋮d\left(2\right)\)

Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\) \(5.\left(12n+1\right)-2.\left(30n+2\right)⋮d\)

\(\Rightarrow1⋮d\)

\(\Rightarrow d=1\)

Mà phân số tối giản thì có \(\text{Ư}CLN\) của tử số và mẫu số là 1

Vậy \(\dfrac{12n+1}{30n+2}\) là phân số tối giản

a) Câu hỏi của ☪Ņĥøķ Ņģøç☪ - Toán lớp 6 - Học toán với OnlineMath