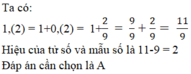c: \(-0.4\left(6\right)=-\dfrac{7}{15}\)

d: \(1,\left(09\right)=\dfrac{12}{11}\)

a: \(-1,\left(3\right)=-\dfrac{4}{3}\)

b: \(0,\left(72\right)=\dfrac{8}{11}\)

0,(4)=4/9

1,(2)=11/9

0,0(8)=4/45

0,1(2)=11/90

\(1,2\left(3\right)=\frac{407}{330}\)

\(2,0\left(6\right)=\frac{31}{15}\)

Bạn thử chỉ mk cả cách làm cụ thể hơn ik

\(1,2\left(3\right)=1,2+0,0\left(3\right)=\frac{6}{5}+\frac{33}{990}=\frac{6}{5}+\frac{11}{330}=\frac{407}{330}\)

\(2,0\left(6\right)=2+0,0\left(6\right)=2+\frac{66}{990}=2+\frac{1}{15}=\frac{31}{15}\)

sao mình k thấy nó hiện lên câu trả lời nhỉ ???

sao ko có câu trả lời vậy

đề nghị ad xem lại

a)Ta có: \(m^3+3m^2+2m+5=m.\left(m^2+3m+2\right)+5\)

                                                       \(=m.\left[m.\left(m+1\right)+2.\left(m+1\right)\right]+5\)

                                                       \(=m.\left(m+1\right).\left(m+2\right)+5\)

Gọi \(d\) là ƯCLN của  \(m.\left(m+1\right).\left(m+2\right)+5\) và \(m.\left(m+1\right).\left(m+2\right)+6\) 

\( \implies\) \(m.\left(m+1\right).\left(m+2\right)+5\) chia hết cho d và \(m.\left(m+1\right).\left(m+2\right)+6\) chia hết cho \(d\)

\( \implies\) \(\left[m.\left(m+1\right).\left(m+2\right)+6\right]-\left[m.\left(m+1\right).\left(m+2\right)+5\right]\) chia hết cho \(d\)

\( \implies\) \(1\) chia hết cho \(d\) 

\( \implies\) \(d=1\) 

\( \implies\)  \(m.\left(m+1\right).\left(m+2\right)+5\) và \(m.\left(m+1\right).\left(m+2\right)+6\) nguyên tố cùng nhau 

Vậy \(A\) là phân số tối giản

b)Ta thấy : \(m;m+1;m+2\) là \(3\) số tự nhiên liên tiếp nên nếu \(m\) chia \(3\) dư \(1\) thì \(m+2\) chia hết cho \(3\) ; nếu  \(m\) chia \(3\) dư \(2\) thì \(m+1\) chia hết cho \(3\)

 Do đó : \(m.\left(m+1\right).\left(m+2\right)\) chia hết cho \(3\) . Mà \(6\) chia hết cho \(3\)

\( \implies\) \(m.\left(m+1\right).\left(m+2\right)+6\) có ước nguyên tố là \(3\) 

Vậy \(A\) là số thập phân vô hạn tuần hoàn 

1,42(16)=3487/4950