Viết chương trình tính các tổng sau: a) S=1+2+3+4+...+n b) S=1+3+5+...+n-1 c) S=2+4+6+...2n

Những câu hỏi liên quan
viết chương trình tính tổng
s= 1*2/3*4+2*3/4*5+3*4/5*6+...+n*(n+1)/(n+2)*(n+3)
uses crt;
var s:real;
i,n:integer;
begin
clrscr;
readln(n);
s:=0;
for i:=1 to n do
s:=s+(n*(n+1))/((n+2)*(n+3));
writeln(s:4:2);
readln;
end.
Đúng 2
Bình luận (0)
a, Sử dụng NNLT Python để viết chương trình tính tổng s=2+4+6+…+n, với n nhập từ bàn phím.
b, Sử dụng NNLT Python để viết chương trình tính tổng s=1+3+5+…+n, với n nhập từ bàn phím.
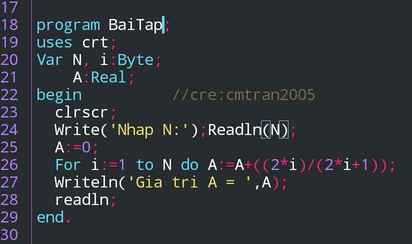
Mô tả thuật toán và viết chương trình tính tổng: S= 2/3+4/5+6/7+...+ 2n/2n+1
Thuật toán: B1: Nhập N;
B2: A <--- 0; i <--- 1;
B3: A <--- A + ((2*i)/(2*i+1));
B4: i <--- i + 1;
B5: Nếu i > N thì thông báo A rồi kết thúc.
B6: Quay lại bước 3;
Đúng 2
Bình luận (0)
Bài 2: a) Tính tổng các số lẻ có hai chữ số b) Tính tổng các số chẵn có hai chữ số c) Tính: S = 1 + 3 + 5 +... + 2n +1 với (n € N) d) Tính: S = 2 + 4 + 6 +...+ 2n với (n € N*)
Viết chương trình tính tổng sau S=1-2+3-4.....-n
Viết thân thôi hen
Var n,i,s:integer;
Read(n);
s:=0;
For i:=1 to n do
If i mod 2 <>0 then s:=s+i else s:=s-i;
Write(s);
end.
Đúng 1
Bình luận (0)
Câu 1: Hãy viết thuật toán cho các biểu thức sau:
a) S= 1+2+3+4+...+n
b)S= 2+4+6+8+...+2n
c)S= 1+3+5+....+(2n+1)
d)S=1+1/2+1/3+1/4+...+1/n
e) S= 1+1/3+1/5+1/7+...+1/2n+1
p.s: mai mk thi rồi giúp mình với T-T
cho số tự nhiên N(1 N<10^6). Tính tổng sau : S= 1-2+3-4+5-6...+N
viết chương trình ra giúp vs
uses crt;
var i,n:integer;
s:longint;
begin
clrscr;
write('nhap n:');readln(n);
s:=0;
for i:=1 to n do
if i mod 2=1 then s:=s+i
else s:=s-i;
writeln('s= ',s);
readln;
end.
Đúng 1
Bình luận (0)
Viết chương trình tính tổng A/ S= 1+1+1+1+1 B/ S = 1+2+3+4+5
b: uses crt;
var s,i:integer;
begin
clrscr;
s:=0;
for i:=1 to 5 do
s:=s+i;
writeln(s);
readln;
end.
Đúng 0
Bình luận (0)
tính tổng;
a,s=1+2+3+4+....+100
b,s=1+2+3+....+n
c,a=1+3+5+....+99
d,b=2+4+6+....+100
e,c=1+3+5+...+[2n+1][n thuộc n*]
f,d=2+4+6+...+2n
giúp tôi với
1 + 2 + 3 + ... + 100
= (100 + 1).100 : 2
= 101.50
= 5050
Đúng 0
Bình luận (0)
a) \(S=1+2+3+4+...+100\)
\(S=\frac{\left(100+1\right)\left[\left(100-1\right):1+1\right]}{2}\)
\(S=5050\)
b) \(S=1+2+3+...+n\)
\(S=\frac{\left(n+1\right)\left[\left(n-1\right):1+1\right]}{2}\)
c) \(A=1+3+5+...+99\)
\(A=\frac{\left(99+1\right)\left[\left(99-1\right):2+1\right]}{2}\)
\(A=2500\)





















