Cho $\triangle A B C$ có $A B<A C$. Tia phân giác của $\widehat{A}$ cắt đường thẳng vuông góc với $B C$ tại trung điểm của $B C$ ở $D$. Gọi $H$ và $K$ là chân các đường vuông góc kẻ từ $D$ đến các đường thẳng $A B$, $A C$. Chứng minh $B H=C K$.

Những câu hỏi liên quan
Trên các cạnh $A B, B C, C A$ của $\triangle A B C$ lấy các điểm $A^{\prime}, B^{\prime}, C^{\prime}$ sao cho $\dfrac{A A^{\prime}}{A B}=\dfrac{B B^{\prime}}{B C}=\dfrac{C C^{\prime}}{A C}$. Chứng minh các tam giác $\triangle A B C$ và $\triangle A^{\prime} B^{\prime} C^{\prime}$ có chung trọng tâm.
The sides of a triangle are a, b and c respectively. What is the perimeter of the triangle if a = 5cm, b = 4cm, and c = 3cm? Answer: The perimeter of the triangle is cm.
Cho $\widehat{xOy}$. Lấy các điểm $A, \, B$ thuộc tia $O x$ sao cho $O A>O B$. Lấy các điểm $C, \, D$ thuộc $O y$ sao cho $O C=O A, \, O D=O B$. Gọi $E$ là giao điểm của $A D$ và $B C$. Chứng minh rằng
a) $A D=B C$.
b) $\triangle A B E=\triangle C D E$.
c) $O E$ là tia phân giác của $\widehat{x O y}$.
a)
Xét \(\Delta AOD\) và \(\Delta COB\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{O}:chung\\OB=OD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOD=\Delta COB\left(c.g.c\right)\)
\(\Rightarrow AD=BC\left(\text{2 cạnh tương ứng}\right)\left(\text{đpcm}\right)\)
b)
Nối A với C
Ta có: \(\left\{{}\begin{matrix}OA=OC\\OB=OD\end{matrix}\right.\left(gt\right)\Rightarrow OA-OB=OC-OD\)
Hay \(AB=CD\)
Xét \(\Delta ABC\) và \(\Delta CDA\) có: \(\left\{{}\begin{matrix}AB=CD\left(cmt\right)\\AC:chung\\AD=BC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABC=\Delta DCA\left(c.c.c\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{CDA}\left(\text{2 góc tương ứng}\right)\)
Vì \(\Delta AOD=\Delta COB\left(cmt\right)\Rightarrow\widehat{A}=\widehat{C}\left(\text{2 góc tương ứng}\right)\)
Xét \(\Delta ABE\) và \(\Delta CDE\) có: \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{CDA}\left(cmt\right)\\AB=CD\left(cmt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABE=\Delta CDE\left(g.c.g\right)\left(\text{đpcm}\right)\)
c) Vì \(\Delta ABE=\Delta CDE\left(cmt\right)\Rightarrow AE=CE\left(\text{2 cạnh tương ứng}\right)\)
Xét \(\Delta AOE\) và \(\Delta COE\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\\AE=CE\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOE=\Delta COE\left(c.g.c\right)\\ \Rightarrow\widehat{AOE}=\widehat{COE}\left(\text{2 góc tương ứng}\right)\)
`=> OE` là phân giác của \(\widehat{xOy}\) (đpcm)
Đúng 2
Bình luận (1)
a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
COE
(hai góc tương ứng)
là tia phân giác của .
Đúng 0
Bình luận (0)
a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
(hai góc tương ứng)
là tia phân giác của .
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
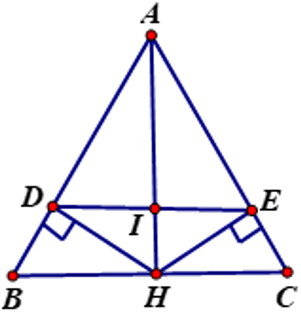
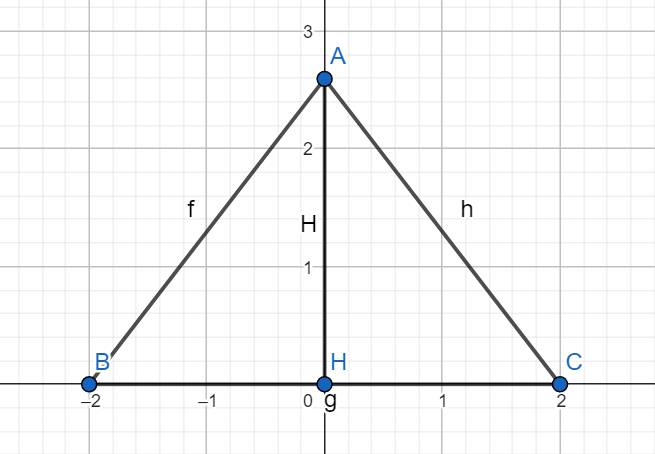
Câu 16: Cho tam giác $ABC$ có $AB=AC$ và tia phân giác góc $A$ cắt $BC$ ở $H$.
a) Chứng minh $\triangle A B H=\triangle A C H$;
b) Chứng minh ${AH} \perp {BC}$;
c) Vẽ ${HD} \perp {AB}$, $(D \in A B)$ và ${HE} \perp {AC}$, $(E \in A C)$. Chứng minh: ${HD}={HE}$.
a) Xét ΔABH và ΔACH có:
AH cạnh chung
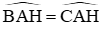
AB = AC (gt)
=> ΔABH = ΔACH (c – g – c)
c.
Gọi I là giao điểm của AH và DE
Xét hai tam giác vuông: ΔADH và ΔAEH có:
AH cạnh chung
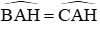
Suy ra: ΔADH = ΔAEH (ch – gn)
Xét ΔADI và ΔAEI có:
AI: cạnh chung
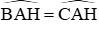
AD = AE (ΔADH = ΔAEH)
=> ΔADI = ΔAEI (c – g – c)
=>\(\left\{{}\begin{matrix}AD=AE\\\widehat{DAI}=\widehat{EAI}\end{matrix}\right.\)
Xét tam giác ADH và tam giác AEH có:
AD = AE
góc DAI = góc EAI
=> tam giác ADH = tam giác AEH (c.g.c)
=> HD = HE (đcpcm)
Đúng 0
Bình luận (0)
GT:tam giác ABC,AB=AC
A cắt BC tại H
KL:a)CM:tam giác ABH=tam giác ACH
b)CM:AH vuông góc BC
c)CM:HD=HE
Đúng 0
Bình luận (0)

a)
Vì △ABC có AB = AC
\(\rightarrow\)B = C
\(\rightarrow\) △ABC là tam giác cân (2 cạnh đáy bằng nhau)
Xét △ABH và △ ACH có:
AC chung
AB = AC (gt)
BH = CH (H là trung điểm của BC)
\(\Rightarrow\) △ABH = △ACH
b)
Có △ABH = △ACH (câu a)
\(\rightarrow\)góc BAH = góc CAH(2 góc tương ứng)
Mà góc BAH + góc CAH = 180 độ (2 góc kề bù)
\(\rightarrow\) góc BAH = góc CAH = 90 độ
\(\Rightarrow\) AH ⊥ BC
c)
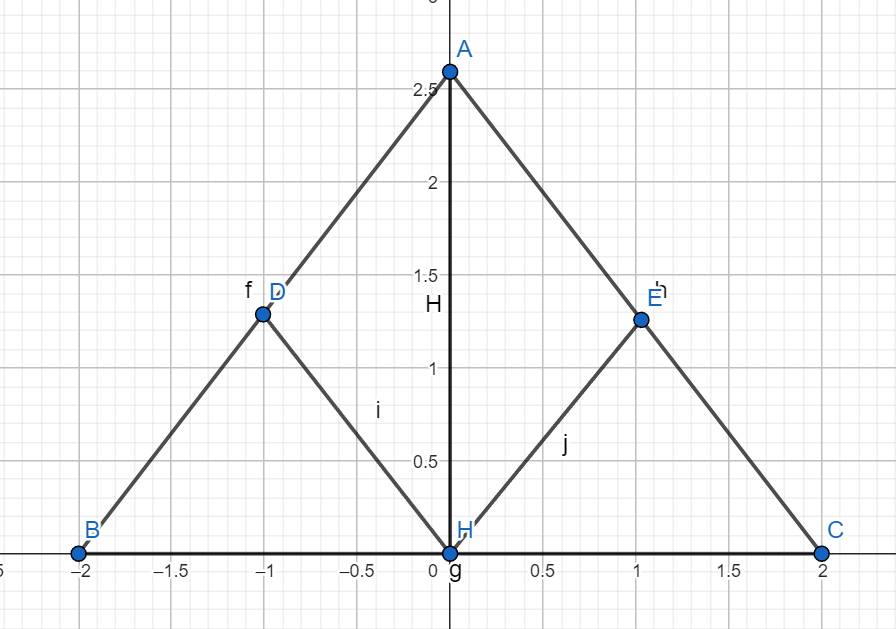
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) Một bồn chứa nước đạng hình trụ có đường kính đáy bằng $1,4m$ và chiều cao bằng $1,5m$. Tinh thể tich của bồn chứa nước đó?
b) Cho $\triangle A B C$ vuông tại $A$ có $A B=3cm, A C=4cm$. Tinh diện tích xung quanh của hình tạo thành khi quay tam giác $A B C$ quanh cạnh $A C$ cố định của nó.
a)V=0,735.π(m3)
b) 5(cm)
- Thể tích của bồn chứa nước đó là 0,735 (m3)
- Diện tích xung quanh là : 15π (cm2)
A /Vậy V=0.735π(m3)
B/vậy Sxq=15π(cm2)
∆ABC vuông tại A;BC=√Ab2+AC2=5cm
Xem thêm câu trả lời
Cho $\triangle ABC$ thoả mãn: $\sin B . \cos ^3 C=\sin C . \cos ^3 B$. Chứng minh rằng $\triangle ABC$ cân.
Câu 4 (3,0 điểm) Cho AABC cân tại A, kẻ đường cao AP a) Chứng minh: triangle ABP sim triangle ACP và P là trung điểm của BC. b) Trên tia đối của tia PA lấy điểm N sao cho PA = PN Chứng minh: AAPH và ACNP, tur dó suy ra AB //CN c) Cho FE vuông góc AB tại E. Chứng minh PE + AB > PA + PB
a: Xet ΔABP vuông tại P và ΔACP vuông tại P có
AB=AC
AP chung
=>ΔABP=ΔACP
b: Xét tứ giác ABNC có
P là trung điểm chung của AN và BC
=>ABNC là hình bình hành
=>AB//NC
Đúng 0
Bình luận (2)
6. A. distribute B. tribe C. trial D. triangle 7. A. decent B. present C. absent D. recent 8. A. disease B. excursion C. divisible D. design 9. A. courageous B. southern C. flourish D. nourish 10. A. naked B. walked ...
Đọc tiếp
6. A. distribute B. tribe C. trial D. triangle
7. A. decent B. present C. absent D. recent
8. A. disease B. excursion C. divisible D. design
9. A. courageous B. southern C. flourish D. nourish
10. A. naked B. walked C. scared D. needed
I Find the word which has a different sound in the underlined part.
Đúng 0
Bình luận (0)
Cho $\triangle A B C$ với $I, J, K$ lần lượt được xác định bời $\overrightarrow{I B}=2 \overrightarrow{I C} ; \overrightarrow{J C}=-\dfrac{1}{2} \overrightarrow{J A} ; \overrightarrow{K A}=-\overrightarrow{K B}$.
a) Tính $\overrightarrow{I J} ; \overrightarrow{I K}$ theo $\overrightarrow{A B} ; \overrightarrow{A C}$.
b) Chứng minh ba điểm $I, J, K$ thẳng hàng.
???????????????????????????????????????????????????????????????
b) Ta có :
\(IB=2IC\Leftrightarrow IB=2\left(IB+BC\right)\Leftrightarrow-IB=2BC\Leftrightarrow BI=2BC\)
\(JC=-\frac{1}{2}JA\Leftrightarrow JB+BC=-\frac{1}{2}\left(JB+BA\right)\)
\(\Leftrightarrow\frac{3}{2}JB=-\frac{1}{2}BA-BC\Leftrightarrow JB=-\frac{1}{3}BA-\frac{2}{3}BC\)
\(\Rightarrow BJ=\frac{1}{3}BA+\frac{2}{3}BC\)
\(\Rightarrow IJ=BJ-BI=\frac{1}{3}BA+\frac{2}{3}BC-2BC=\frac{1}{3}BA-\frac{4}{3}BC\)
\(KA=-KB\Leftrightarrow KB+BA=-KB\Leftrightarrow2KB=-BA\)
\(\Rightarrow2BK=BA\Leftrightarrow BK=\frac{1}{2}BA\)
\(\Rightarrow JK=BK-BJ=\frac{1}{2}BA-\frac{2}{3}BC=\frac{1}{6}BA-\frac{2}{3}BC\)
\(=\frac{1}{2}\left(\frac{1}{3}BA-\frac{4}{3}BC\right)=\frac{1}{2}IJ\)
Vậy \(I,J,K\)thẳng hàng
ài 2. Cho hình chóp SABC có triangle ABC vuông tại B. Biết SA L (ABC). a) Chứng minh: BC L (SAB); b) Gọi BK là đường cao trong triangle ABC . Chứng minh BK 1 (SAC); 2) Gọi AH là đường cao của Delta*S . Chứng minh: AH L SC.
a: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
b: BK vuông góc AC
BK vuôg góc SA
=>BK vuông góc (SAC)
Đúng 0
Bình luận (0)