Tìm x nguyên để mỗi phân số sau có giá trị nhỏ nhất
B= -5/(x+3)^2+1
Tìm giá trị nguyên dương của x để đa thức sau có giá trị nhỏ nhất
B= /x-3/ + /x+4/
B=|3-x|+|x+4|>=|3-x+x+4|=7
Dấu = xảy ra khi -4<=x<=3
a=x+5/x+1 b=2x+4/x+3 c=3x+8/x-1 d=2x-3/x-1 e=5x+9/x+5 g=4x+9/2x+1 h=6x+5/2x-1 i=4x-6/2x+1 k=4x+4/2x+4 n=4x+6/2x+2
tìm giá trị nhỏ nhất
B= (x^2+1) (y^2+1) - (x+4) (x-4) - ( y-5) (y+5)
A= (x-1) (x+2) (x+3) (x+6)
\(B=\left(x^2+1\right)\left(y^2+1\right)-\left(x-4\right)\left(x+4\right)-\left(y-5\right)\left(y+5\right)\\ B=x^2y^2+x^2+y^2+1-x^2+16-y^2+25\\ B=x^2y^2+41\ge41\)
Dấu "=" xảy ra khi \(x^2y^2\Leftrightarrow x=y=0\)
Vậy \(MaxB=41\Leftrightarrow x=y=0\)
\(A=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\\ A=\left[\left(x-1\right)\left(x+6\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]\\ A=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\\ A=\left(x^2+5x\right)^2-36\ge-36\)
Dấu "=" xảy ra khi
\(\left(x^2+5x\right)^2=0\\ \Leftrightarrow x\left(x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy \(MaxA=-36\Leftrightarrow x\in\left\{0;-5\right\}\)
Tìm x nguyên để mỗi phân số sau có giá trị là số tự nhiên:
a, \(\dfrac{x-2}{x+3}\)
Cảm ơn nha!
Ta có:\(\dfrac{x-2}{x+3}=\dfrac{x+3-5}{x+3}=1-\dfrac{5}{x+3}\)
Để bt có giá trị là số tự nhiên thì \(5⋮x+3\Rightarrow x+3\inƯ_{\left(5\right)}=\left\{\pm1;\pm5\right\}\)
| x + 3 | 1 | -1 | 5 | -5 |
| x | -2 | -4 | 2 | -8 |
| Kết luận | thỏa mãn | loại | thỏa mãn | loại |
=> \(x=\pm2\)
Giải:
a) \(\dfrac{x-2}{x+3}\)
Để \(\dfrac{x-2}{x+3}\) là số tự nhiên thì \(x-2⋮x+3\)
\(x-2⋮x+3\)
\(\Rightarrow x+3-5⋮x+3\)
\(\Rightarrow5⋮x+3\)
\(\Rightarrow x+3\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Ta có bảng giá trị:
| x+3 | -5 | -1 | 1 | 5 |
| x | -8 | -4 | -2 | 2 |
Ta thấy:
Nếu \(x\in\left\{-8;-4;2\right\}\) thì \(\dfrac{x-2}{x+3}\) sẽ là số tự nhiên
Vậy \(x\in\left\{-8;-4;2\right\}\)
Chúc bạn học tốt!
Bài 1:Tìm số nguyên x để 5/x+3 đạt giá trị lớn nhất
Bài 2:Tìm số nguyên x để biểu thức A=x-13/x+3 có giá trị nhỏ nhất
Bài 3:Tìm số nguyên x để biểu thức B=7-x/x-5 đạt giá trị lớn nhất
giúp mình với.Mình cảm ơn các bạn
Toán lớp 6
Tìm số nguyên của x để mỗi phân thức sau có giá trị là số nguyên:
a) (x^4 - 2x^3 - 3x^2 + 8x - 1) / (x^2 - 2x +1)
b) (x^4 + 3x^3 +2x^2 + 6x -2) / (x^2 + 2)
MK ko biế đúng ko nữa , sai thì ý kiến
a)
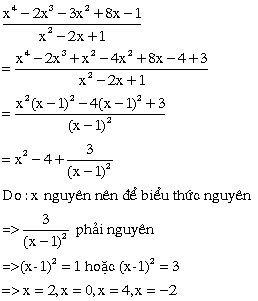
b)
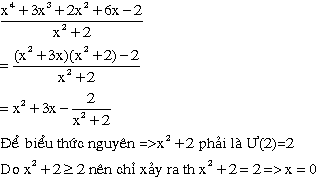
Chúc các bn hok tốt
Tham khảo nhé
Cho biểu thức:A=\(\dfrac{2x-1}{x+2}\)
a) Tìm số nguyên x để biểu thức A là phân số
b)Tìm các số nguyên x để biểu thức A có giá trị là 1 số nguyên
c)Tìm các số nguyên x để biểu thức A đạt giá trị lớn nhất,giá trị nhỏ nhất
A = \(\dfrac{2x-1}{x+2}\)
a, A là phân số ⇔ \(x\) + 2 # 0 ⇒ \(x\) # -2
b, Để A là một số nguyên thì 2\(x-1\) ⋮ \(x\) + 2
⇒ 2\(x\) + 4 - 5 ⋮ \(x\) + 2
⇒ 2(\(x\) + 2) - 5 ⋮ \(x\) + 2
⇒ 5 ⋮ \(x\) + 2
⇒ \(x\) + 2 \(\in\) { -5; -1; 1; 5}
⇒ \(x\) \(\in\) { -7; -3; -1; 3}
c, A = \(\dfrac{2x-1}{x+2}\)
A = 2 - \(\dfrac{5}{x+2}\)
Với \(x\) \(\in\) Z và \(x\) < -3 ta có
\(x\) + 2 < - 3 + 2 = -1
⇒ \(\dfrac{5}{x+2}\) > \(\dfrac{5}{-1}\) = -5 ⇒ - \(\dfrac{5}{x+2}\)< 5
⇒ 2 - \(\dfrac{5}{x+2}\) < 2 + 5 = 7 ⇒ A < 7 (1)
Với \(x\) > -3; \(x\) # - 2; \(x\in\) Z ⇒ \(x\) ≥ -1 ⇒ \(x\) + 2 ≥ -1 + 2 = 1
\(\dfrac{5}{x+2}\) > 0 ⇒ - \(\dfrac{5}{x+2}\) < 0 ⇒ 2 - \(\dfrac{5}{x+2}\) < 2 (2)
Với \(x=-3\) ⇒ A = 2 - \(\dfrac{5}{-3+2}\) = 7 (3)
Kết hợp (1); (2) và(3) ta có A(max) = 7 ⇔ \(x\) = -3
1. Tìm các giá trị nguyên của x để các biểu thức sau có giá trị lớn nhất
a. A=1/7-x b.B=27-2x/12-X
2.Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nhỏ nhất
a. A=1/x-3 b. B= 7-x/x-5 c. C= 5x-19/x-4
3.Tìm giá trị nhỏ nhất của các biếu thức sau
a. A=x^4+3x^2 +2 b. B=(x^4+5)^2 c. C=(x-1)^2+(y+2)^2
4.Tìm giá trị lớn nhất của các biểu thức sau
a. A=5-3(2x-1)^2 b.B=1/2(x-1)^2+3 c. C=x^2+8/x^2+2
Tìm giá trị nguyên của x để mỗi biểu thức sau có giá trị là một số nguyên:
a) A= 2x^3+x^2+4x+5 / 2x+1
b) B= x^3 / 6+x^2 / 2+x^3