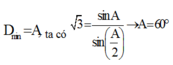Lăng kính có chiết suất \(\sqrt{3}\), góc chiết quang 60 o. Chiếu tia sáng qua mặt bên lăng kính với góc tới 30 o.
a. Tính góc ló lệch về phía đáy của lăng kính
b. Tính góc lệch tạo bởi tia ló và tia tới
Một tia sáng tới vuông góc với mặt bên của một lăng kính có chiết suất n = 2 và góc chiết quang A = 30 0 . Góc lệch của tia sáng qua lăng kính là:
A. D = 13 0 .
B. D = 22 0 .
C. D = 5 0 .
D. D = 15 0 .
Đáp án D
+ Tia sang truyền vuông góc với mặt bên lăng kính, sẽ truyền thẳng vào bên trong.
+ Tại mặt bên thứ hai, ta có n sin i = sin r ⇔ 2 sin 30 ° = sin r ⇔ r = 45 ° .
Góc lệch D = 45 ° - 30 ° = 15 ° .
Một tia sáng tới vuông góc với mặt AB của một lăng kính có chiết suất n = 2 và góc chiết quang A = 30 0 . Góc lệch của tia sáng qua lăng kính là:
A. D = 5 0
B. D = 13 0
C. D = 15 0
D. D = 22 0
Đáp án cần chọn là: C
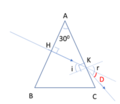
Tia sáng chiếu tới AB vuông góc tại H nên truyền thẳng tới AC tại K
Xét tam giác AHK vuông tại H có = 30 0 → AKH ^ = 60 0 → i = 30 0 (1)
Ta có, tại mặt bên AC: sin i g h = 1 n = 1 2 → i g h = 45 0 (2)
Từ (1) và (2): i < sin i g h → tia sáng truyền tại mặt bên AC tại K bị khúc xạ ra ngoài không khí với góc lệch D như hình vẽ: D = r – i (3)
Áp dụng định luật khúc xạ ánh sáng tại mặt AC ta có:
n . sin i = sinr → 2 sin 30 = sinr → sinr = 2 2 → r = 45 0
Thay vào (3) → D = 15 0
Một lăng kính có góc chiết quang A. Chiếu tia sáng SI đến vuông góc với mặt bên của lăng kính. Biết góc lệch của tia ló và tia tới là D = 15 ° . Cho chiết suất của lăng kính là n = 4 3 . Tính góc chiết quang A?
Chiếu một tia sáng tới vuông góc với mặt bên của lăng kính thủy tinh có chiết suất tuyệt đối n = 1,5, góc chiết quang A. Tia ló hợp với tia tới một góc D = 30 o Góc chiết quang của lăng kính là:
A. A = 23 o 24 '
B. A = 41 o
C. A = 38 o 16 '
D. A = 66 o
Chiếu một tia sáng tới vuông góc với mặt bên của lăng kính thủy tinh có chiết suất tuyệt đối n = 1,5, góc chiết quang A. Tia ló hợp với tia tới một góc D = 30 o Góc chiết quang của lăng kính là:
A. 23 o 24 '
B. 41 o
C. 38 o 16 '
D. 66 o
Một lăng kính có góc chiết quang A. Chiếu tia sáng SI đến vuông góc với mặt bên của lăng kính. Biết góc lệch của tia ló và tia tới là D = 15 0 . Cho chiết suất của lăng kính là n = 1,5 . Góc chiết quang A bằng:
A. 25,87 0
B. 64,13 0
C. 23 0
D. 32 0
Đáp án cần chọn là: A
Vì chiếu tia tới vuông góc với mặt nên i 1 = 0 → r 1 = 0
Ta có: A = r 1 + r 2 → A = r 2
Mà: D = i 1 + i 2 − A ↔ 15 = 0 + i 2 − A → i 2 = 15 + A
Lại có:
sin i 2 = n sinr 2 ↔ sin i 2 = n sin A ↔ sin ( 15 + A ) = 1,5 sin A
↔ sin 15 c osA + sinAcos 15 = 1,5 sin A
↔ sin 15 c osA = ( 1,5 − cos 15 ) sinA
→ tan A = sin 15 1,5 − c os 15 = 0,485 → A = 25,87
Lăng kính có chiết suất n = 2 và góc chiết quang A = 60 0 . Một chùm tia sáng đơn sắc hẹp được chiếu vào mặt bên AB của lăng kính với góc tới . Tính góc ló của tia sáng khi ra khỏi lăng kính và góc lệch của tia ló và tia tới.
A. 20 0
B. 30 0
C. 40 0
D. 50 0
Đáp án cần chọn là: B
Theo bài ra: i 1 = 45 0 , n = 2
sin i 1 = n sin r 1 ⇒ sin 45 0 = 2 sin r 1 ⇒ r 1 = 30 0 ⇒ r 2 = A – r 1 = 30 0
n sin r 2 = sin i 2 ⇒ 2 sin 30 0 = sin i 2 ⇒ i 2 = 45 0
Góc lệch: D = ( i 1 + i 2 ) – A = 30 0
Một lăng kính có góc chiết quang 6 ° , chiết suất 1,6 đặt trong không khí. Chiếu một tia sáng đơn sắc tới mặt bên của lăng kính với góc tới rất nhỏ. Góc lệch của tia sáng qua lăng kính là
A. không xác định được
B. 6 °
C. 3 °
D. 3 , 6 °
Đáp án D.
Khi góc tới nhỏ, ta có sin của một góc sấp xỉ bằng góc đó
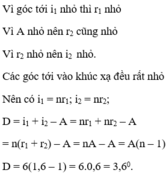
Lăng kính có thiết diện là một tam giác có góc chiết quang A đặt trong không khí. Biết chiết suất của lăng kính là n= 3 . Chiếu tia sáng đơn sắc tới mặt bên thứ nhất và cho tia ló ra khỏi mặt bên thứ hai. Biết góc lệch cực tiểu của tia sáng qua lăng kính bằng góc chiết quang. Tính góc chiết quang.
A. 450.
B. 600.
C. 750.
D. 300.
Đáp án B
+ Khi có góc lệch cực tiểu thì
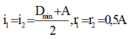
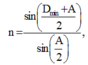với 
