∆ABC có M là trung điểm của BC.
Trên tia đối của tia MA lấy điểm N sao cho MN = MA.
Ta có:
ےAMB = ےNMC (đối đỉnh)
BM = CM (giả thiết)
MA = MN (dựng hình)
Suy ra: ∆MAB = ∆MNC (c.g.c)
Suy ra: NC = AB và ےMBA = ےMCN
Do ےMBA = ےMCN nên AB // NC
Suy ra ےBAC + ےACN = 180
Ta có: ےBAC = 90 nên ےACN = 90
=> ∆ABC = ∆CNA (c.g.c) vì AC là cạnh chung
AB = NC (cmt) và ےBAC = ےACN = 90
=> AN = BC
=> AM = \(\frac{1}{2}BC\)

=>CMT

Ta có: tam giác ABC vuông tại A,M là trung điểm của BC (gt) => AM là đg trung tuyến ứng vs cạnh huyền BC của tam giác vuông ABC

=>AM = 1/2 BC ( trong tam giác vuông, đg trung tuyến ứng vs cạnh huyền bằng nửa cạnh huyền )

Vậy....

vẽ thêm MD song song AH

MH song song AD

Xét tam giác MDA và tam giác AHM có

Góc A1 = góc M2 (so le trong)

Góc A2 = góc M1 ( so le trong)

AM là cạnh chung

\(\Rightarrow\)Tam giác MDA = tam giác AHM (g.c.g)

\(\Rightarrow\)MD = AH (2 cạnh tương ứng)

Xét tam giác MBD và tam giác CMH có

Góc BMD = góc MCH (đồng vị)

Góc D1 = góc H2 (=90)

BM = MC (giả thiết)

\(\Rightarrow\)Tam giác MBD = tam giác CMH (cạnh huyền - góc nhọn)

\(\Rightarrow\)BD = MH ( 2 cạnh tương ứng)

Xét tam giác BDM và tam giác MHA có

MD = AH ( cmt)

Góc D2 = góc H1 (=90)

BD = MH (cmt)

\(\Rightarrow\)tam giác MBD = tam giác MAH ( c.g.c)

\(\Rightarrow\)BM = AM (2 cạnh tương ứng)

Vì BM = MC và AM = BM

\(\Rightarrow\)AM = MC

Mà BC = BM + MC

\(\Rightarrow\)BC = 2*AM

\(\Rightarrow\)AM = \(\frac{1}{2}\cdot BC\)

Vậy AM = \(\frac{1}{2}\cdot BC\)

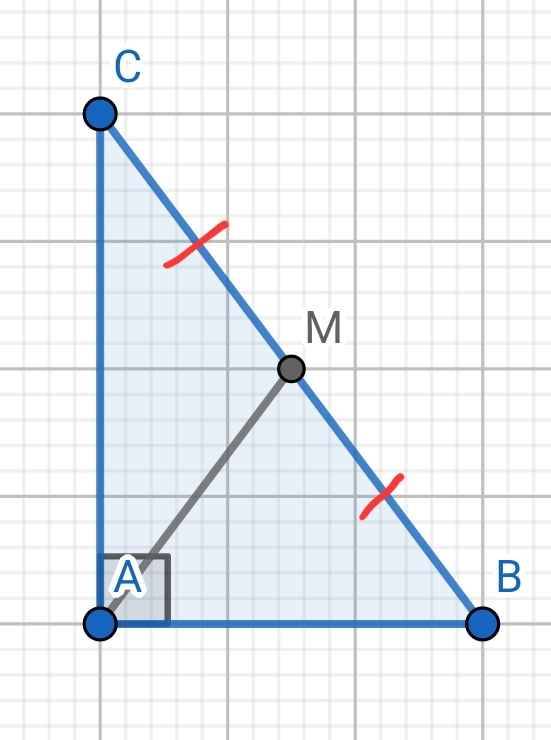
a) ∆ABC vuông tại A

M là trung điểm BC

⇒ AM là đường trung tuyến ứng với cạnh huyền BC

⇒ AM = BM = CM = BC : 2

b) ∆ABC vuông tại A có ∠C = 30⁰

⇒ ∠B = 90⁰ - 30⁰ = 60⁰

Do AM = BM (cmt)

⇒ ∆ABM cân tại M

Lại có ∠ABM = ∠B = 60⁰

⇒ ∆ABM đều

⇒ AB = AM = BM = BC : 2

GT: Δ ABC vuông tại A

BM = CM

D ϵ tia đối của tia MA sao cgo MA = MD

KL: AD = BC

\(AM=\frac{1}{2}BC\)

Ta có hình vẽ:

Nối đoạn BD

Xét Δ BMD và Δ CMA có:

BM = CM (gt)

BMD = CMA (đối đỉnh)

MD = MA (gt)

Do đó, Δ BMD = Δ CMA (c.g.c)

=> BD = AC (2 cạnh tương ứng) và BDM = MAC (2 góc tương ứng)

Mà BDM và MAC là 2 góc so le trong nên BD // AC

=> BAC + ABD = 180^o (trong cùng phía)

=> 90^o + ABD = 180^o

=> ABD = 180^o - 90^o = 90^o = BAC

Xét Δ ABD và Δ BAC có:

BD = AC (cmt)

ABD = BAC = 90^o

AB là cạnh chung

Do đó, Δ ABD = Δ BAC (c.g.c)

=> AD = BC (2 cạnh tương ứng) (1)

Mà AM = MD = \(\frac{1}{2}AD\) (2)

Từ (1) và (2) => \(AM=\frac{1}{2}BC\left(đpcm\right)\)

Tứ giác ABCD có M là trung điểm của BC và AD

=> Tứ giác ABCD là hình bình hành có góc A=90⁰

=> Hình bình hành ABCD là hình chữ nhật.

=> AD=BC

=> AM=DM=BM=CM

Mà BM + MC = BC

=> AM= 1/2 BC