Giải phuơng trình: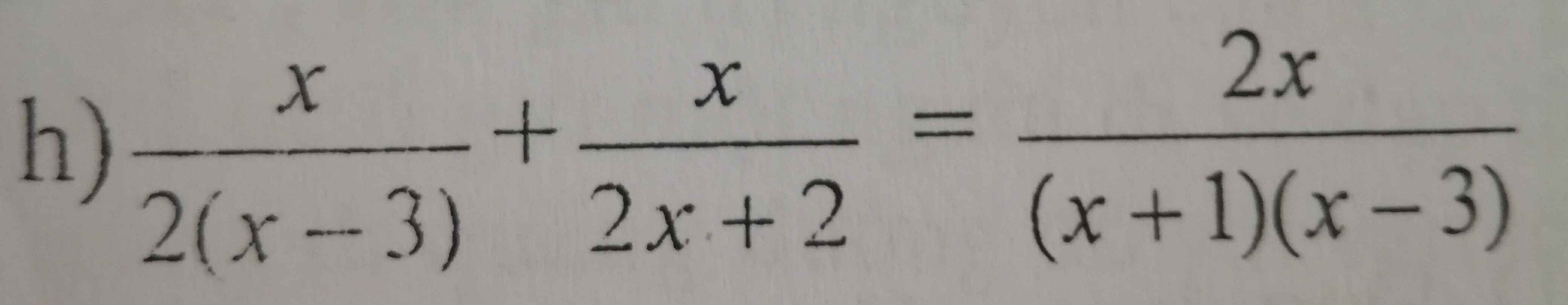

Những câu hỏi liên quan
giải phuơng trình nghiệm nguyên x+y+xy=x^2+y^2.4.2x^2+4x=19-3y^2
x+4y=6 căn 2
x+y=3
giải hệ phuơng trình
Giải phuơng trình :X \(^2\)+2(y\(^2\)+1)=2X(Y+1)
giải phuơng trình \(2\left(x^2+2x+3\right)=5\sqrt{x^3+3x^2+3x+2}\)
giải phuơng trình
\(\sqrt[3]{x^2-1}+x=\sqrt{x^3-2}\)
help me mik cần gấp
Giải bài toán bằng cách phuơng trình hoc hệ phương trình:
Tìm một số tự nhiên có hai chữ số. Biết chữ số hàng chục lớn hơn chữ số hàng đơn vị là 3 và tổng các bình phương của hai chữ số là 45 .
Gọi chữ số hàng chục là của số cần tìm là \(x\)(điều kiện: \(3< x\le9;x\inℕ\)).
Chữ số hàng đơn vị của số cần tìm là \(x-3\).
Vì tổng các bình phương của 2 chữ số là \(45\) nên ta có phương trình:
\(x^2+\left(x-3\right)^2=45\).
\(\Leftrightarrow x^2+x^2-6x+9-45=0\).
\(\Leftrightarrow2x^2-6x-36=0\).
\(\Leftrightarrow2\left(x^2-3x-18\right)=0\).
\(\Leftrightarrow x^2-3x-18=0\).
\(\Leftrightarrow\left(x-6\right)\left(x+3\right)=0\).
\(\Leftrightarrow\orbr{\begin{cases}x-6=0\\x+3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=6\left(tm\right)\\x=-3\left(ktm\right)\end{cases}}\)(tm: Thỏa mãn; ktm: Không thỏa mãn).
\(\Leftrightarrow x=6\).
Do đó chữ số hàng đơn vị của chữ số cần tìm là \(6-3=3\).
Vậy số cần tìm là \(63\)
Bài làm :
Gọi x ; y lần lượt là chữ số hàng chục và chữ số hàng đơn vị .
Điều kiện : \(x,y\inℕ;x>3\)
Theo đề bài ; ta có hệ phương trình ;
\(\hept{\begin{cases}x=y+3\\x^2+y^2=45\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=y+3\\\left(y+3\right)^2+y^2=45\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=y+3\\y^2+6y+9+y^2-45=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=y+3\\2y^2+6y-36=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=y+3\\y^2+3y-18=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=6\\y=3\end{cases}}\)
Vậy số cần tìm là 63
Gội số hàng chục là x (10>x>3) ⇒ Số hàng đơn vị là x-3
Mà tổng các bình phương của hai chữ số là 45 nên ta có phương trình:
x2+(x-3)2=45
Giải ra ta được x=6 (thỏa mãn) hoặc x=-3(loại)
⇒Chữ số hàng đơn vị là 6-3=3
Vậy số cần tìm là 63
Xem thêm câu trả lời
{x + 5y = 10 { y= -x²/ 200
Giải gíup mik hệ phuơng trình này đi
\(\begin{cases}x+5y=10\left(1\right)\\y=-\frac{x^2}{200}\left(2\right)\end{cases}\)(1)<=>5y=10-x
2 vế của pt (1) chia 5 ta có:
\(y=\frac{10-x}{5}\).Thay pt (2) vào (1) ta có:
\(-\frac{x^2}{200}=\frac{10-x}{5}\Leftrightarrow-x^2\cdot5=\left(10-x\right)\cdot200\)
\(\Leftrightarrow-5x^2=2000-200x\)
\(\Leftrightarrow5x^2-200x+2000=0\)
\(\Leftrightarrow5\left(x^2-40x+400\right)=0\)
\(\Leftrightarrow x^2-40x+400=0\)
\(\Leftrightarrow\left(x-20\right)^2=0\)
\(\Leftrightarrow x=20\).Thay vào (2) ta có: \(y=\frac{-20^2}{200}=2\)
Vậy hệ phương trình trên có nghiệm là \(\begin{cases}x=20\\y=2\end{cases}\)
Đúng 0
Bình luận (0)
(x-2)(x2-3x+5)= (2-x)(1-x2)
Giair phuơng trình nhé
\(\left(x-2\right)\left(x^2-3x+5\right)=\left(2-x\right)\left(1-x^2\right)\\ \Leftrightarrow\left(x-2\right)\left(x^2-3x+5\right)=-\left(x-2\right)\left(1-x^2\right)\\ \Leftrightarrow\left(x-2\right)\left(x^2-3x+5\right)+\left(x-2\right)\left(1-x^2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x^2-3x+5+1-x^2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(-3x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\-3x+6=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=2\end{matrix}\right.\\ \Leftrightarrow x=2\)
Đúng 1
Bình luận (0)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+5\right)=-\left(x-2\right)\left(1-x^2\right)\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+5\right)+\left(x-2\right)\left(1-x^2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+5+1-x^2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(6-3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=2\end{matrix}\right.\)
Vậy \(S=\left\{2\right\}\)
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên của phuơng trình sau: 2xy-x-y=1
Ta có: 2xy - x - y = 1
=> x(2y-1) - y =1 => 2x(2y-1) - 2y = 2 => 2x(2y-1) - (2y-1) = 3
=> (2y-1)(2x-1) = 3
Ta có bảng:
| 2y-1 | 1 | -1 | 3 | -3 |
| 2x-1 | 3 | -3 | 1 | -1 |
| x | 2 | -1 | 1 | -1 |
| y | 1 | 0 | 2 | 0 |
Đúng 1
Bình luận (0)
Xem thêm câu trả lời




















