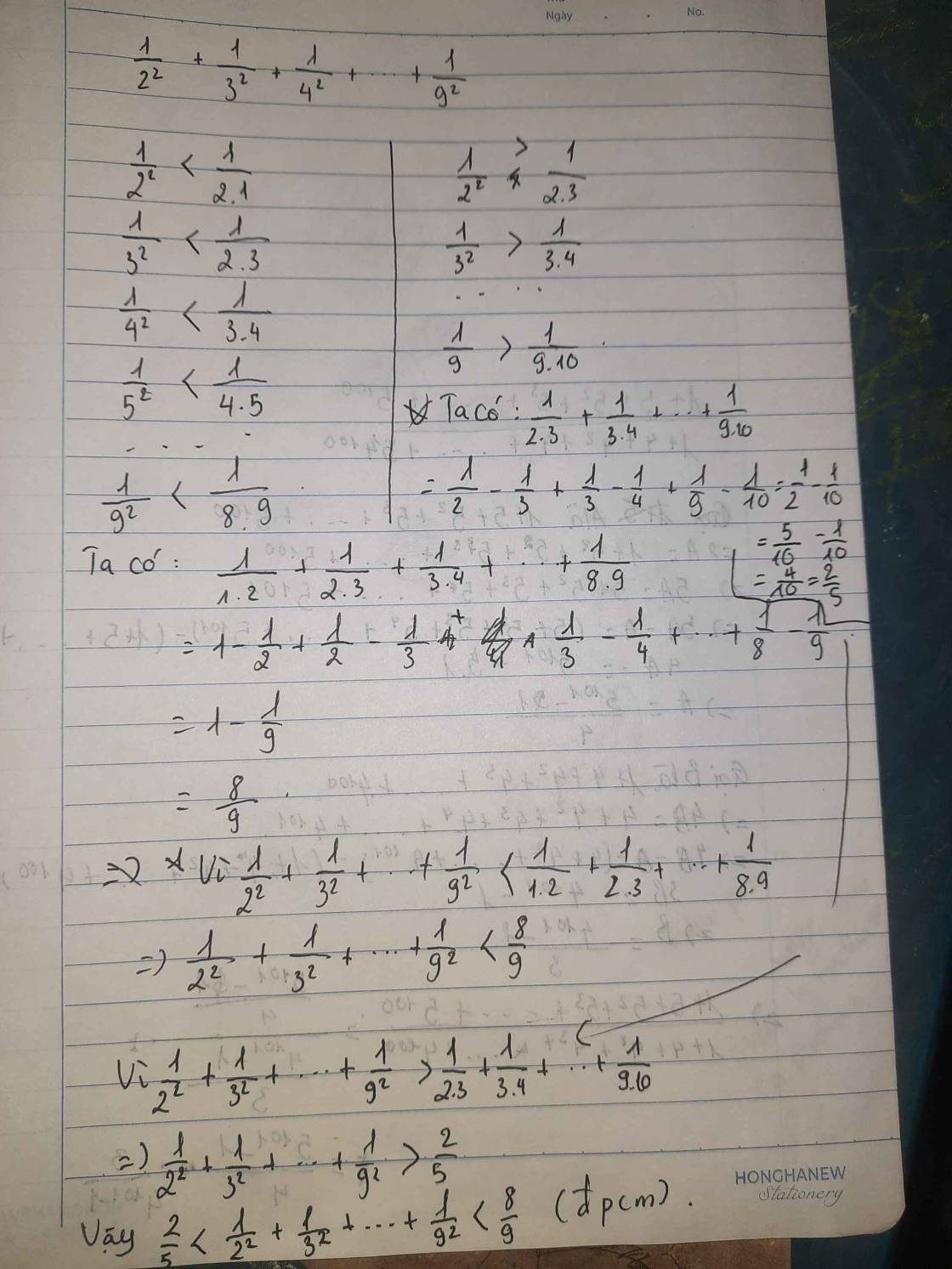Những câu hỏi liên quan
cho S = 1/5^2 + 1/7^2 + 1/9^2+...+1/103^2
Chứng minh rằng S < 5/32
Mọi người giúp mik với ạ. Cảm ơn
a,Cho a∈N, a>1. Chứng minh rằng 1/a-1/a+1<1/a2<1/a-1-1/a
b, Cho S= 1/22+1/32+1/42+...+1/92.Chứng minh rằng 2/5<S<8/9
BÀI 3*
a.Cho S=1/31+1/32+1/33+...+1/60 . Chứng minh rằng 3/5<S<4/5
b. Cho M =1/2^2+1/3^2+1/4^2+...+1/9^2. Chứng minh rằng 2/5<S<8/9
CÁC BẠN GIÚP MÌNH VỚI
BẠN NÀO NHANH MÌNH TICK CHO!
Cho S = 1/2^2 + 1/3^2 + 1/4^2 +...+ 1/9^2
chứng minh rằng 2/5 < S < 8/9
cho : S = 1/2^2 + 1/3^2 + 1/4^2 + 1/5^2 +......+ 1/9^2 chứng minh rằng 2/5 < S < 8 / 9
Ta có S=1/2^2+1/3^2+1/4^2+...+1/9^2
<1/2²+1/2*3+1/3*4+....+1/8*9
=1/2²+1/2-1/3+1/3-1/4+....+1/8-1/9
=1/4+1/2-1/9=23/36<32/36=8/9 (♪)
Ta lại có S=1/2^2+1/3^2+1/4^2+...+1/9^2
>1/2²+1/3*4+1/4*5+....+1/9*10
=1/2²+1/3-1/4+1/4-1/5+........+1/9-1/10
=1/2²+1/3-1/10
=19/20>8/20=2/5 ( ♫)
Từ (♪)( ♫) cho ta đpcm
Đúng 4
Bình luận (0)
Xem thêm câu trả lời
S=1/2^2+1/3^2+1/4^2+....+1/9^2.Chứng minh rằng 2/5 < S <8/9
S=1/2^2 + 1/3^2 + 1/4^2 +...+ 1/9^2. Chứng minh rằng 2/5 < S <8/9
Xem thêm câu trả lời
S=1/2^2+1/3^2+1/4^2+....+1/9^2
chứng minh rằng:2/5<S<8/9
S<1/2^2 + 1/2.3 + 1/3.4 +...+ 1/8.9
S<1/4 + 1/2 - 1/3 + 1/3 - 1/4+...+1/8 - 1/9
S<1/4 + 1/2 - 1/9
S<23/36<8/9 (1)
Mặt khác: S>1/2^2 + 1/3.4 + ...+ 1/9*10
S>1/4 + 1/3 - 1/4 + ... + 1/9 - 1/10
S>1/4 + 1/3 - 1/10
S>29/60>2/5 (2)
Từ (1),(2)
=> 2/5<S<8/9
Đúng 0
Bình luận (1)
Cho S=1/2+1/3+1/4+...+1/31+1/32 a) chứng minh rằng S>5/2 b) chứng minh rằng S<9/2
`Answer:`
\(S=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{31}+\frac{1}{32}\)
a) Ta thấy:
\(\frac{1}{3}+\frac{1}{4}>\frac{1}{4}+\frac{1}{4}=\frac{1}{2}\)
\(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{1}{2}\)
\(\frac{1}{9}+...+\frac{1}{16}>8.\frac{1}{16}=\frac{1}{2}\)
\(\frac{1}{17}+\frac{1}{18}+...+\frac{1}{32}>16.\frac{1}{32}=\frac{1}{2}\)
\(\Rightarrow S>\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{5}{2}\)
b) Ta thấy:
\(\frac{1}{3}+\frac{1}{4}+\frac{1}{5}< 3.\frac{1}{3}\)
\(\frac{1}{6}+...+\frac{1}{11}< 6.\frac{1}{6}\)
\(\frac{1}{12}+...+\frac{1}{23}< 12.\frac{1}{12}\)
\(\frac{1}{24}+...+\frac{1}{32}< 9.\frac{1}{24}\)
\(\Rightarrow S< \frac{1}{2}+1+1+1+\frac{9}{24}=\frac{31}{8}< \frac{9}{2}\)