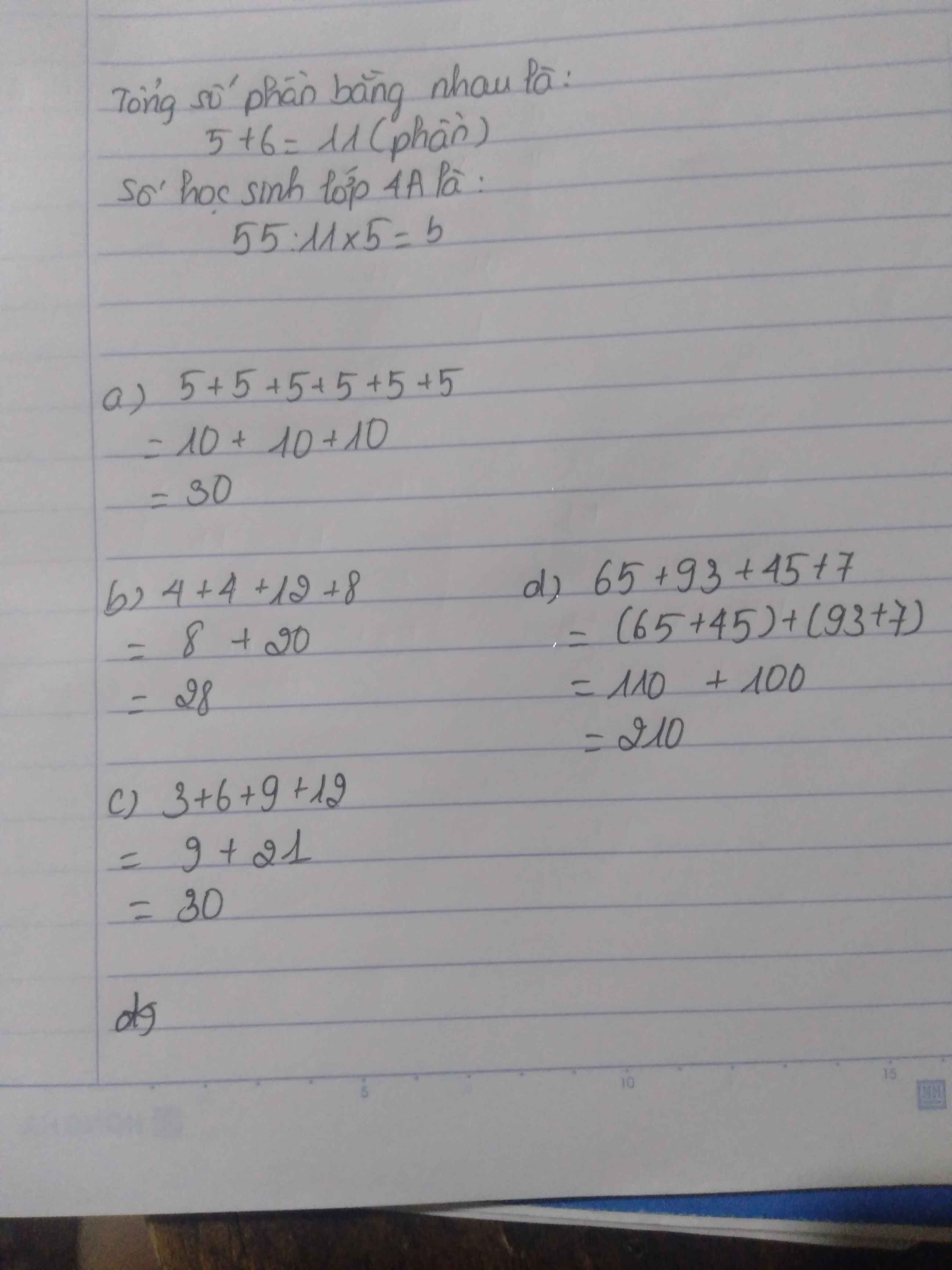S=(99-97)+(95-93)+.......+(3-1)

S=2+2+......+2(25 số hạng)

S=2x25

S=50

Mình tính 1 dãy S thôi nhá -_-

Số số hạng của dãy : ( 99 - 1 ) : 2 + 1 = 50 số

Mỗi cặp có 2 số hạng => Có số cặp là : 50 : 2 = 25 cặp

Mỗi cặp có kết quả = 2 => Kết quả = 2 x 25 = 50

Tổng S có SSH là:

       ( 99-1):2+1=50(số hạng)

=>Tổng S có số cặp là:

        50:2=25(cặp)

 Ta có:

S=(99-97)+(95-93)+(91-89)+...+((11-9)+(7--5)+(3-1)

S=2+2+2+...+2

S=2.50

S=100

Ta có : \(\dfrac{2x+5}{95}+\dfrac{2x+6}{94}+\dfrac{2x+7}{93}=\dfrac{2x+93}{7}+\dfrac{2x+94}{6}+\dfrac{2x+95}{5}\)

\(\Leftrightarrow\dfrac{2x+5}{95}+\dfrac{2x+6}{94}+\dfrac{2x+7}{93}-\dfrac{2x+93}{7}-\dfrac{2x+94}{6}-\dfrac{2x+95}{5}=0\)

\(\Leftrightarrow\dfrac{2x+5}{95}+1+\dfrac{2x+6}{94}+1+\dfrac{2x+7}{93}+1-\dfrac{2x+93}{7}-1-\dfrac{2x+94}{6}-1-\dfrac{2x+95}{5}-1=0\)

\(\Leftrightarrow\dfrac{2x+100}{95}+\dfrac{2x+6}{94}+\dfrac{2x+7}{93}-\dfrac{2x+100}{7}-\dfrac{2x+100}{6}-\dfrac{2x+100}{5}=0\)

\(\Leftrightarrow\left(2x+100\right)\left(\dfrac{1}{95}+\dfrac{1}{94}+\dfrac{1}{93}-\dfrac{1}{7}-\dfrac{1}{6}-\dfrac{1}{5}\right)=0\)

Thấy : \(\dfrac{1}{95}+\dfrac{1}{94}+\dfrac{1}{93}-\dfrac{1}{7}-\dfrac{1}{6}-\dfrac{1}{5}\ne0\)

\(\Rightarrow2x+100=0\)

\(\Leftrightarrow x=-50\)

Vậy ...

Ta có: \(\dfrac{2x+5}{95}+\dfrac{2x+6}{94}+\dfrac{2x+7}{93}=\dfrac{2x+93}{7}+\dfrac{2x+94}{6}+\dfrac{2x+95}{5}\)

\(\Leftrightarrow\dfrac{2x+5}{95}+1+\dfrac{2x+6}{94}+1+\dfrac{2x+7}{93}+1=\dfrac{2x+93}{7}+1+\dfrac{2x+94}{6}+1+\dfrac{2x+95}{5}+1\)

\(\Leftrightarrow\dfrac{2x+100}{95}+\dfrac{2x+100}{94}+\dfrac{2x+100}{93}=\dfrac{2x+100}{7}+\dfrac{2x+100}{6}+\dfrac{2x+100}{5}\)

\(\Leftrightarrow\left(2x+100\right)\left(\dfrac{1}{95}+\dfrac{1}{94}+\dfrac{1}{93}\right)=\left(2x+100\right)\left(\dfrac{1}{7}+\dfrac{1}{6}+\dfrac{1}{5}\right)\)

\(\Leftrightarrow\left(2x+100\right)\left(\dfrac{1}{95}+\dfrac{1}{94}+\dfrac{1}{93}\right)-\left(2x+100\right)\left(\dfrac{1}{7}+\dfrac{1}{6}+\dfrac{1}{5}\right)=0\)

\(\Leftrightarrow\left(2x+100\right)\left(\dfrac{1}{95}+\dfrac{1}{94}+\dfrac{1}{93}-\dfrac{1}{7}-\dfrac{1}{6}-\dfrac{1}{5}\right)=0\)

mà \(\dfrac{1}{95}+\dfrac{1}{94}+\dfrac{1}{93}-\dfrac{1}{7}-\dfrac{1}{6}-\dfrac{1}{5}\ne0\)

nên 2x+100=0

\(\Leftrightarrow2x=-100\)

hay x=-50

Vậy: S={-50}

\(A=5+5^2+5^3+5^4+...+5^{2022}\\ =\left(5+5^2+5^3+5^4+5^5+5^6\right)+....+5^{2016}\left(5+5^2+5^3+5^4+5^5+5^6\right)\\ =19530+....+5^{2016}.19530\\ =210.93+...+5^{2016}.210.93\\ =93.210.\left(1+...+5^{2016}\right)⋮93\left(ĐPCM\right)\)

Đáp án C

a)5+5+5+5+5+5=6x5=30                                           b)4+4+12+8=4x7=28

c) 3+6+9+12=3x10=30                                        d)65 + 93 + 35 + 7 =5x40

a. 30

b. 28

c. 30

d. 200

\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{91.93}+\frac{1}{x}=5\)

\(\Rightarrow\left(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{91.93}\right)+\frac{1}{x}=5\)

\(\Rightarrow\left[\frac{1}{2}\times\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{91.93}\right)\right]+\frac{1}{x}=5\)

\(\Rightarrow\left[\frac{1}{2}\times\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{91}-\frac{1}{93}\right)\right]+\frac{1}{x}=5\)

\(\Rightarrow\left[\frac{1}{2}\times\left(1-\frac{1}{93}\right)\right]+\frac{1}{x}=5\)

\(\Rightarrow\left[\frac{1}{2}\times\frac{92}{93}\right]+\frac{1}{x}=5\)

\(\Rightarrow\frac{46}{93}+\frac{1}{x}=5\)

\(\Rightarrow\frac{1}{x}=5-\frac{46}{93}\)

\(\Rightarrow\frac{1}{x}=\frac{419}{93}\)

\(\Rightarrow x=1:\frac{419}{93}\)

\(\Rightarrow x=\frac{93}{419}\)

Vậy  \(x=\frac{93}{419}\)

_Chúc bạn học tốt_

chậc

ai mà bít