Cho tam giác ABC điểm D nằm giữa B và C chứng minh rằng (AB+AC-BC):2<AD

Những câu hỏi liên quan
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng:
a)AD>AB+AC-BC/2
b)AD<AB+AC-BC/2
Cho tam giác ABC có B > 90o, điểm D nằm giữa B và C. Chứng minh rằng AB < AD < AC
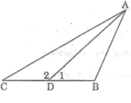
Trong ∆ABD ta có: ∠B > 90o
⇒ ∠B > ∠D1 ( trong 1 tam giác, góc tù là góc lớn nhất- chú ý tổng ba góc trong một tam giác bằng 180º) ⇒ AD > AB (đối diện góc lớn hơn là cạnh lớn hơn) (1)
Trong ΔABD ta có: ∠D2 là góc ngoài tại đỉnh D nên ∠D2 = ∠B + ∠BAD. Suy ra: ∠D2 > ∠B > 90o
Trong ΔADC ta có: ∠D2 > 90o
⇒ ∠D2 > ∠C ⇒ AC > AD (cạnh đối diện góc lớn hơn là cạnh lớn hơn) (2)
Từ (1) và (2) suy ra: AB < AD < AC
Đúng 0
Bình luận (0)
Tam giác ABC có AB < AC Tia phân giác của góc A cắt bc ở D chứng minh rằng điểm D nằm giữa 2 điểm B và M (M là trung điểm của BC)
Tam giác ABC có AB < AC Tia phân giác của góc A cắt bc ở D chứng minh rằng điểm D nằm giữa 2 điểm B và M (M là trung điểm của BC)
Cho ABC (AB < AC). Gọi D là điểm nằm giữa A và B, E là điểm nằm giữa A và C và BD = CE. Gọi M, N, I lần lượt là trung điểm của BC, DE, BE.. a)Đường thẳng MN cắt đường thẳng AB ởP, cắt đường thẳng AC ởQ. Chứng minh tam giác APQ cân.b )Kẻphân giác AF của tam giác ABC. Chứng minh MN // AF.
Cho tam giác ABC có B > 90o, điểm D nằm giữa B và C. Chứng minh rằng AB < AD < AC
Cho tam giác ABC cân tại A, trên cạnh BC lấy điểm D và E sao cho BD=CE(D nằm giữa B và E)
a)Chứng minh tam giác ABD bằng tam giác ACE
b)Kẻ DM vuông góc với AB(M thuộc AB) và EN vuông góc với AC(N thuộc AC). CHứng minh AM=AN
c) Gọi K là giao điểm của đường thẳng DM và đường thẳng EN và góc BAC = 120 độ, chứng minh rằng tam giác DKE là tam giác đều
Câu a (1,0đ) Chứng minh :![]() ABD =
ABD = ![]() ACE
ACE
Xét ![]() ABD và
ABD và![]() ACE :có AB=AC (cạnh bên
ACE :có AB=AC (cạnh bên ![]() cân);
cân); ![]() =
=![]() (góc đáy
(góc đáy![]() cân);BD=CE (gt) (0,25đ) x3=(0,75đ)
cân);BD=CE (gt) (0,25đ) x3=(0,75đ)
Vậy ![]() ABD =
ABD = ![]() ACE(cgc) (0,25đ)
ACE(cgc) (0,25đ)
Câu b (0,75đ) Chứng minh đúng ![]() vuông AMD =
vuông AMD = ![]() vuông ANE vì có AD = AE;
vuông ANE vì có AD = AE; ![]()
(do ![]() ABD =
ABD =![]() ACE) (0,5đ)
ACE) (0,5đ)
Kết luận ![]() AMD =
AMD =![]() ANE và suy ra AM =AN) (0,25đ)
ANE và suy ra AM =AN) (0,25đ)
Câu c (0,75đ): Chứng minh đúng ![]() vuông BMD =
vuông BMD =![]() vuông CNE (cạnh huyền - góc nhọn )(0,25đ)
vuông CNE (cạnh huyền - góc nhọn )(0,25đ)
Lập luận chứng minh được ![]() rồi suy ra
rồi suy ra ![]() KDE cân tại K (1)(0,25đ)
KDE cân tại K (1)(0,25đ)
Từ ![]() lập luận để
lập luận để ![]()
![]() (2)
(2)
Kết hợp (1)và (2) ![]()
![]() KDE đều )(0,25đ)
KDE đều )(0,25đ)
Đúng 0
Bình luận (0)
https://olm.vn/hoi-dap/question/1231127.html
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, trên cạnh BC lấy điểm D và E sao cho BD=CE(D nằm giữa B và E) a)Chứng minh tam giác ABD bằng tam giác ACE b)Kẻ DM vuông góc với AB(M thuộc AB) và EN vuông góc với AC(N thuộc AC). CHứng minh AM=AN c) Gọi K là giao điểm của đường thẳng DM và đường thẳng EN và góc BAC = 120 độ, chứng minh rằng tam giác DKE là tam giác đều
a) Xét tam giác ABD và tam giác ACE có:
AB = AC (Vì tam giác ABC cân tại A)
\(\widehat{ABC}=\widehat{ACB}\)(vì tam giác ABC cân tại A)
BD = CE (gt)
Do đó tam giác ABD = tam giác ACE(cgc)
b) Ta có: tam giác ABD = tam giác ACE (cmt)
\(\Rightarrow\)AD = AE (hai cạnh tương ứng) (1)
\(\Rightarrow\widehat{BAD}=\widehat{CAE}\)(hai góc tương ứng) (2)
Từ (1) và (2) \(\Rightarrow\) tam giác vuông AMD = tam giác vuông ANE (ch-gn)
\(\Rightarrow\)AM = AN (hai cạnh tương ứng)
c) Trong tam giác ABC có góc BAC=120 độ
\(\Rightarrow\)Góc ABC = góc ACB = \(\frac{180-120}{2}\)= 30 độ
Trong tam giác vuông BMD có góc MBD = 30 độ \(\Rightarrow\widehat{MDB}=60\)độ
Tương tự: Ta được, trong tam giác vuông NCE có góc NEC =60 độ
\(\Rightarrow\)\(\widehat{MDB}=\widehat{NEC}\)(=60 độ)
Mặt khác: \(\widehat{MDB}=\widehat{EDK}\left(đđ\right)\)
\(\widehat{NEC}=\widehat{DEK}\left(đđ\right)\)
\(\Rightarrow\widehat{EDK}=\widehat{DEK}\)(=60 độ)
\(\Rightarrow\widehat{DKE}=180-\left(60\times2\right)=60\)độ
\(\Rightarrow\)Trong tam giác DKE có 3 góc EDK;DEK;DKE cùng bằng 60
Hay tam giác DKE đều.
Đúng 2
Bình luận (0)
a) Xét hai tam giác ABD và ACE ta có
AB = AC (gt)
\(\widehat{ABD}=\widehat{ACE}\left(gt\right)\)
BD = CE (gt)
Do đó: \(\Delta ABD=\Delta ACE\left(c-g-c\right)\)
b) Ta có: \(\Delta ABD=\Delta ACE\)(câu a)
\(=>\hept{\begin{cases}\widehat{BAD}=\widehat{EAC}\\AD=AE\end{cases}}\)(cặp góc và cặp cạnh tương ứng)
Xét hai tam giác vuông AMD và ANE ta có
AD = AE (cmt)
\(\widehat{MAD}=\widehat{EAN}\left(cmt\right)\)
Do đó: \(\Delta AMD=\Delta ANE\left(c.h-g.n\right)\)
=> AM =AN (cặp cạnh tương ứng)
c) Trong \(\Delta ABC\)cân tại A ta có: \(\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{BAC}}{2}=\frac{180^o-120^0}{2}=30^o\)
Trong \(\Delta MDB\)vuông tại M ta có: \(\widehat{BDM}=90^o-\widehat{DBM}=90^o-30^o=60^o\)
Ta lại có: \(\widehat{ABC}=\widehat{ACB}\left(gt\right)\)
=> \(\widehat{MDB}=\widehat{NEC}\)(vì cùng bù với \(\widehat{ABC}\))
mà \(\hept{\begin{cases}\widehat{BDM}=\widehat{KDE}\left(đđ\right)\\\widehat{NEC}=\widehat{DEK}\left(đđ\right)\end{cases}}\)
=> \(\widehat{KDE}=\widehat{KED}=60^o\)(1)
Trong \(\Delta DKE\)có: \(\widehat{KDE}+\widehat{KED}+\widehat{DKE}=180^o\)
hay \(60^o+60^o+\widehat{DKE}=180^o\)
\(120^o+\widehat{DKE}=180^o\)
\(\widehat{DKE}=180^o-120^o\)
\(\widehat{DKE}=60^o\)(2)
Từ (1) và (2) => \(\Delta DKE\)là tam giác đều
P/s: k hộ thần :3
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, trên cạnh BC lấy điểm D và E sao cho BD=CE(D nằm giữa B và E)
a)Chứng minh tam giác ABD bằng tam giác ACE
b)Kẻ DM vuông góc với AB(M thuộc AB) và EN vuông góc với AC(N thuộc AC). CHứng minh AM=AN
c) Gọi K là giao điểm của đường thẳng DM và đường thẳng EN và góc BAC = 120 độ, chứng minh rằng tam giác DKE là tam giác đều













