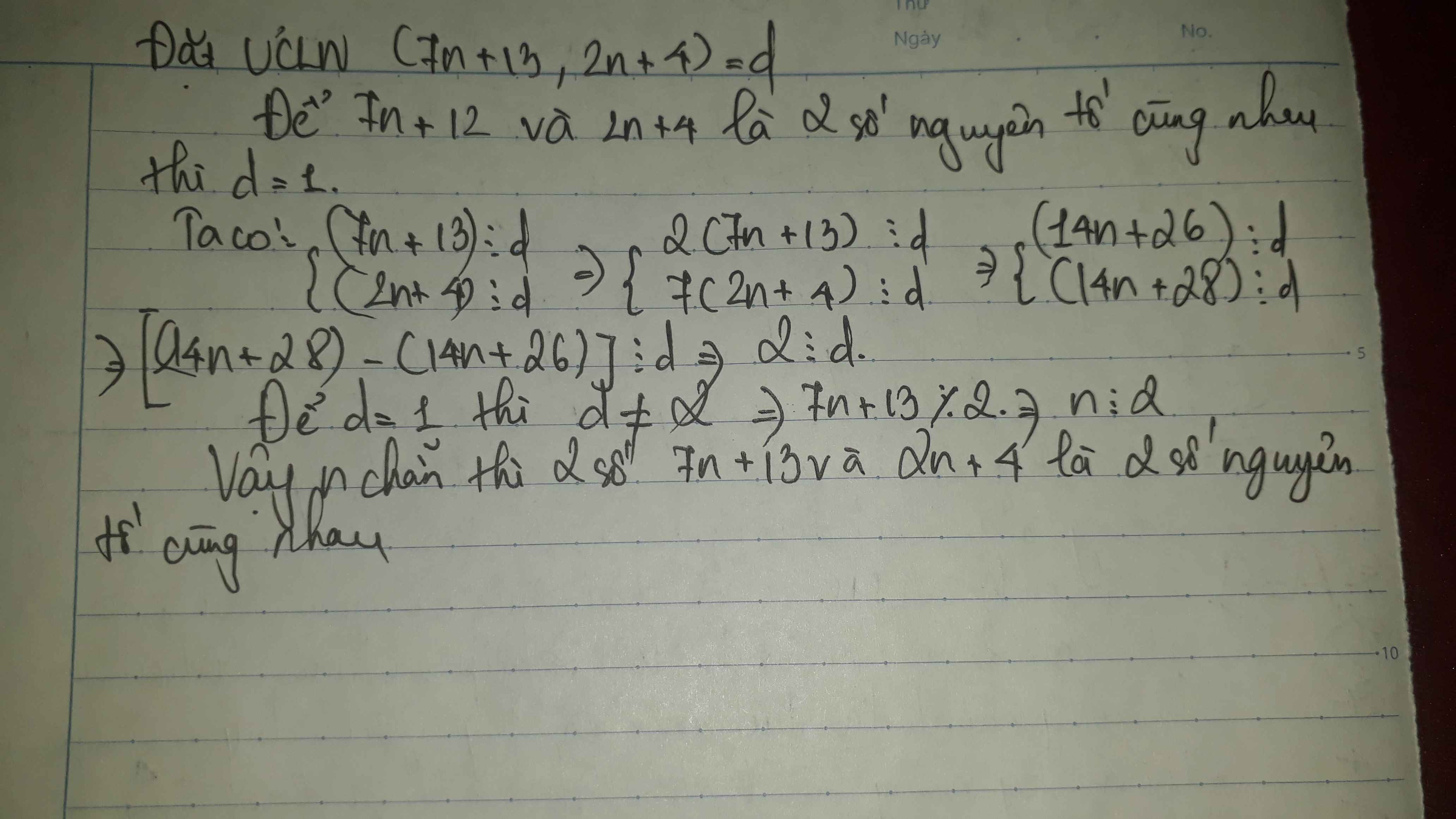Tìm số tự nhiên n để 2n-1 và 2n+1 đồng thời là hai số nguyên tố.

Những câu hỏi liên quan
tìm số tự nhiên n sao cho: n+2; n+10 và 2n+27 đồng thời là số nguYÊN TỐ
Olm sẽ hướng dẫn em giải những dạng toán nâng cao như này bằng phương pháp đánh giá em nhé.
Nếu n = 2 ta có: 2 + 2 = 4 ( loại)
Nếu n = 3 ta có: 2n + 27 = 2.3 + 27 = 33 (loại)
Nếu n > 3 thì vì n là số nguyên tố nên n có dạng:
n = 3k + 1 hoặc n = 3k + 2
Với n = 3k + 1 ta có: n + 2 = 3k + 1 + 2 = 3k + 3 ⋮ 3 (loại)
Với n = 3k + 2 ta có: n + 10 = 3k + 2 + 10 = 3k + 12 =3.(k+4)⋮3 (loại)
Không có số tự nhiên nào thỏa mãn n+2; n+10; 2n+27 đồng thời là số nguyên tố.
Kết luận: n \(\in\) \(\varnothing\)
Đúng 0
Bình luận (0)
tìm số tự nhiên n để 2n+1 và 9n+4 là hai số nguyên tố cùng nhau
tìm số tự nhiên n để 2n+1 và 7n+2 là hai số nguyên tố cùng nhau
Để 2n+1 và 7n+2 là hai số nguyên tố cùng nhau
<=> ƯCLN(2n+1;7n+2) = 1
<=> 7.(2n+1)-2.(7n+2) chia hết cho 1
<=> 14n+7-14n-4 chia hết cho 1
<=> 3 chia hết cho 1
Vậy n = 3 (thỏa mãn \(n\in N\) )
Đúng 0
Bình luận (0)
mik thấy câu rả lời này nhiều lắm,chắc các bn copy của nhau chớ gì.mik cần câu trả lời tự làm của các bn nhưng phải chi tiết ,rõ ràng và chính xác
Đúng 0
Bình luận (0)
Gọi \(\left(2n+1;7n+2\right)=d\)
\(\Rightarrow\hept{\begin{cases}2n+1⋮d\\7n+2⋮d\end{cases}\Rightarrow\hept{\begin{cases}14n+7⋮d\\14n+4⋮d\end{cases}\Rightarrow}\left(14n+7\right)-\left(14n+4\right)⋮d}\)
\(\Rightarrow3⋮d\Rightarrow d\in\left\{1;3\right\}\)
\(d=3\Rightarrow2n+1⋮3\Rightarrow4n+2⋮3\Rightarrow3n+n+2⋮3\)
\(\Rightarrow n+2⋮3\Rightarrow n=3k-2\left(k\inℕ^∗\right)\)
=> d=3 thì rút gọn được
\(\Rightarrow n#3k-2\Rightarrow\)tối giản
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm số tự nhiên n để: 2n+1 và 7n+2 là hai số nguyên tố cùng nhau
Tìm số tự nhiên n để 2n+1 và 7n+2 là hai số nguyên tố cùng nhau.
Để 2n + 1 và 7n + 2 nguyên tố cùng nhau
<=> ƯCLN(2n + 1; 7n + 2) = 1
<=> 7.(2n + 1) - 2.(7n + 2) chia hết cho 1
<=> 14n + 7 - 14n + 4 chia hết cho 1
<=> 3 chia hết cho 1
Vậy n = 3
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
tìm số tự nhiên n để 2n +3 và 4n+1 là hai số nguyên tố cùng nhau
Gọi d€ƯC(2n+3;4n+1)
=>2n+3:d=>2(2n+1):d
=>4n+1:d=>4n+1:d
=>[2(2n+3)-4n+1]:d
=>(4n+6-4n+1):d
=>5:d
=>d€Ư(5)={1;5}
Với d=5=>2n+3:5
=>(2n+3-5):5
=>(2n-2):5
=>2(n-1):5
=>n-1:5(vì 2 không chia hết cho 5)
=>n-1=5k(k€N*)
=>n=5k-1
Thay n=5k+1 vào
4n+1=4.(5k+1)+1
=20k+4+1
=20k+5
Vậy n khác 5k+1 thì 2n+3 và 4n+1 là nguyên tố cùng nhau
Đúng 0
Bình luận (0)
1.Tìm số tự nhiên n để:
a, 2n+1 và 7n+2 là 2 số nguyên tố cùng nhau.
b,9n+24 và 3n+4 là 2 số nguyên tố cùng nhau.
2.Chứng minh rằng 2n+1 và 3n+1 (n là số tự nhiên) là 2 số nguyên tố cùng nhau.
\(Taco::::::::::::::::::::::::::::::::::::::::::::::::::::::::::\)
\(GỌi:ƯCLN\left(2n+1;7n+2\right)=d\Rightarrow7\left(2n+1\right)-2\left(7n+2\right)⋮d\Rightarrow3⋮d\)
Để 2n+1 và 7n+2 nguyên tố cùng nhau thì: 2n+1 hoặc 7n+2 ko chia hết cho 3
Giả sử: 2n+1 chia hết cho 3
=> 2n+1-3 chia hết cho 3
=> 2n-2 chia hết cho 3
=> 2(n-1) chia hết cho 3=> n-1 chia hết cho 3
Giả sử: 7n+2 chia hết cho 3
=> 7n+2-9 chia hết cho 3
=>.........
Vậy với n khác 3k+1;3k+2 thì thỏa mãn
Đúng 1
Bình luận (0)
tìm tất cả n là số tự nhiên để 2n+1, 3n+1 là số chính phương, 2n+9 là số nguyên tố
Do \(2n+1\) và \(3n+1\) là các số chính phương dương nên tồn tại các số nguyên dương a,b sao cho \(2n+1\)\(=a^2\) và \(3n+1=b^2\). Khi đó ta có:
\(2n+9=25.\left(2n+1\right)-16.\left(3n+1\right)=25a^2-16b^2=\left(5a-4b\right).\left(5a+4b\right)\)
Do \(2n+9\) là nguyên tố,\(5a+4b>1\) và \(5a+4b>5a-4b\) nên ta phải có \(5a-4b=1\), tức là: \(b=\dfrac{5a-1}{4}\)
\(\Rightarrow\) ta có: \(\left\{{}\begin{matrix}2n+1=a^2\left(1\right)\\3n+1=\dfrac{\left(5a-1\right)^2}{16}\left(2\right)\end{matrix}\right.\)
Từ (1) : \(2n+1=a^2\Rightarrow n=\dfrac{a^2-1}{2}\) và a > 1 ( do n>0)
Thay vào (2): \(\dfrac{3.\left(a^2-1\right)}{2}+1=\dfrac{\left(5a-1\right)^2}{16}\) => (a - 1).(a - 9) = 0
=> a = 9. Từ đó ta có n = 40
Vậy duy nhất một giá trị n thỏa mãn yêu cầu đề bài là : n = 40
Đúng 7
Bình luận (0)
tìm số tự nhiên n để hai số : 7n+ 13 và 2n+4 là hai số nguyên tố cùng nhau
1.Chứng tỏ rằng hai số lẻ liên tiếp là hai số nguyên tố cùng nhau
2.Chứng minh rằng với mọi số tự nhiên , các số sau là các số nguyên tố cùng nhau.
a) n+1 và n+2 b)2n+2 và 2n+3
c)2n+1 và n+1 d)n+1 và 3n+4
Đọc tiếp
1.Chứng tỏ rằng hai số lẻ liên tiếp là hai số nguyên tố cùng nhau
2.Chứng minh rằng với mọi số tự nhiên , các số sau là các số nguyên tố cùng nhau.
a) n+1 và n+2 b)2n+2 và 2n+3
c)2n+1 và n+1 d)n+1 và 3n+4
Bài 1: Gọi hai số lẻ liên tiếp là $2k+1$ và $2k+3$ với $k$ tự nhiên.
Gọi $d=ƯCLN(2k+1, 2k+3)$
$\Rightarrow 2k+1\vdots d; 2k+3\vdots d$
$\Rightarrow (2k+3)-(2k+1)\vdots d$
$\Rightarrow 2\vdots d\Rightarrow d=1$ hoặc $d=2$
Nếu $d=2$ thì $2k+1\vdots 2$ (vô lý vì $2k+1$ là số lẻ)
$\Rightarrow d=1$
Vậy $2k+1,2k+3$ nguyên tố cùng nhau.
Ta có đpcm.
Đúng 2
Bình luận (0)
Bài 2:
a. Gọi $d=ƯCLN(n+1, n+2)$
$\Rightarrow n+1\vdots d; n+2\vdots d$
$\Rightarrow (n+2)-(n+1)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $(n+1, n+2)=1$ nên 2 số này nguyên tố cùng nhau.
b.
Gọi $d=ƯCLN(2n+2, 2n+3)$
$\Rightarrow 2n+2\vdots d; 2n+3\vdots d$
$\Rightarrow (2n+3)-(2n+2)\vdots d$ hay $1\vdots d$
$\Rightarrow d=1$.
Vậy $(2n+2, 2n+3)=1$ nên 2 số này nguyên tố cùng nhau.
Đúng 2
Bình luận (0)
Bài 2:
c.
Gọi $d=ƯCLN(2n+1, n+1)$
$\Rightarrow 2n+1\vdots d; n+1\vdots d$
$\Rightarrow 2(n+1)-(2n+1)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $ƯCLN(2n+1, n+1)=1$ nên 2 số này nguyên tố cùng nhau.
d.
Gọi $d=ƯCLN(n+1, 3n+4)$
$\Rightarrow n+1\vdots d; 3n+4\vdots d$
$\Rightarrow 3n+4-3(n+1)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $ƯCLN(n+1, 3n+4)=1$
$\Rightarrow$ 2 số này nguyên tố cùng nhau.
Đúng 1
Bình luận (0)