Nhờ thầy cô hướng dẫn giải chi tiết bài này ạ.


Những câu hỏi liên quan
Nhờ thầy cô hướng dẫn giải chi tiết bài 1.e) ở dưới ạ.

a, 41,51,61
b, 70, 90
c, 55, 66, 77
d, 15, 25
e, 34 (Từ số hạng thứ 3 = Tổng 2 số hạng trước nó:22=10+12; Số hạng thứ 4 = Số hạng thứ 2+ Số hạng thứ 3 = 12+22=34)
f, 30, 20
Đúng 2
Bình luận (0)
1,a,41,51,61 d,15,20,25
b,70,90 e, 34 (Từ số hạng thứ 3 = Tổng 2 số hạng trước nó:22=10+12; Số hạng thứ 4 = Số hạng thứ 2+ Số hạng thứ 3 = 12+22=34)
c,55,66,77 f,30,20
Đúng 0
Bình luận (0)
Hiện nay, mẹ 42 tuổi. Tính tuổi con hiện nay, biết rằng lúc mẹ sinh con mẹ 27 tuổi.
Con nhờ thầy cô giáo hướng dẫn giải chi tiết bài toán trên ạ.
Số tuổi mẹ tăng thêm kể từ khi sinh con:
42 - 27 = 15 (năm)
Số tuổi của con bằng số tuổi mẹ tăng thêm nên con 15 tuổi
Đúng 0
Bình luận (0)
Kiến thức quan trọng cần nhớ với các bài toán về tuổi là hiệu số tuổi luôn không đổi theo thời gian em nhé
Giải
Vì mỗi năm mỗi người tăng thêm một tuổi nên hiệu số tuổi của hai mẹ con luôn không đổi theo thời gian.
Mẹ sinh con năm mẹ 27 tuổi vậy mẹ hơn con 27 tuổi, hiện nay mẹ vẫn hơn con 27 tuổi.
Từ những lập luận trên ta có:
Tuổi con hiện nay là: 42 - 27 = 15 (tuổi)
Đáp số: 15 tuổi.
Đúng 2
Bình luận (0)
Có 13 kg gạo, một cân 2 đĩa và một quả cân loại 1 kg. Làm thế nào để chỉ với hai lần cân lấy ra được 4 kg gạo?
Con nhờ thầy cô hướng dẫn giải chi tiết bài toán trên ạ.
Cân lần 1: Đặt quả cân 1kg lên một dĩa cân, đổ 13kg gạo vào hai dĩa cân cho đến khi cân thăng bằng. Vậy ta được một dĩa cân có 6kg và một dĩa cân có 7kg.
Cân lần 2: Đặt quả cân 1kg lên một dĩa cân, đổ 7kg vào hai dĩa cân cho đến khi cân thăng bằng. Vậy ta được một dĩa 3kg và một dĩa có 4kg. Như vậy ta đã cân được 4kg gạo
Đúng 1
Bình luận (0)
Con nhờ thầy cô giáo hướng dẫn giải chi tiết bài toán ở dưới ạ.
Trong phép trừ, nếu tăng số bị trừ thêm 14 đơn vị và số trừ giảm đi 9 đơn vị thì hiệu mới bằng 55. Tìm hiệu trong phép trừ ban đầu. (Số trừ trong phép trừ ban đầu lớn hơn 9)
hiệu khi không giảm số trừ đi 9 là:
55-9=46
hiệu ban đầu là:
46-14=32
Đ/s:32
Đúng 0
Bình luận (0)
Trong túi có 5 viên bi đỏ, 4 viên bi xanh và 3 viên bi vàng. Hỏi không nhìn vào túi, phải lấy ra ít nhất bao nhiêu viên bi để chắc chắn có ít nhất 3 viên bi cùng một màu?
Con nhờ thầy cô giáo hướng dẫn giải chi tiết bài toán trên ạ.
Ít nhất có 3 viên bi cùng màu phải lấy được ít nhất: tất cả số bi vàng, tất cả số bi xanh, 3 bi đỏ
SL ít nhất cần lấy: 3 + 4 + 3 = 10 (viên bi)
Đ.số: 10 viên bi
Đúng 1
Bình luận (0)
Số lượng ít nhất cần lấy là:
\(3+4+3=10\left(viên.bi\right)\)
Đúng 0
Bình luận (0)
Thầy cô và các bạn giúp em câu này với. Hướng cách làm thôi ạ. Ko cần giải chi tiết đâu ạ. Em cảm ơn nhiều.
bạn chỉ cần tách x4-1 thành (x2-1)(x2+1),rồi đặt x2=t là ok
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Thầy cô và các bạn giúp em câu này với. Hướng cách làm thôi ạ. Ko cần giải chi tiết đâu ạ. Em cảm ơn nhiều.
Tính 
Tách sin^2 = 1-cos^2=(1-cos)(1+cos)
Dùng phương pháp đồng nhất hệ số, đưa về thế này
1/cos +1/2(1-cos) -1/2(1+cos)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
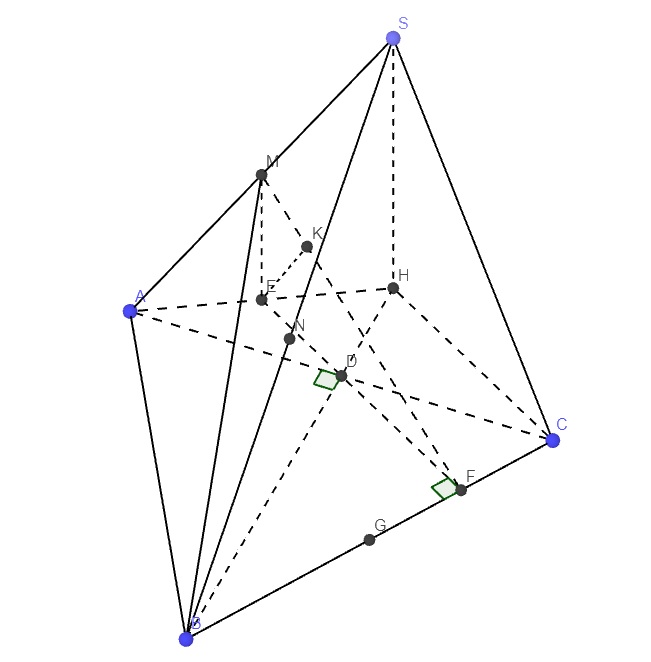
Thầy cô hướng dẫn giúp e bài này ạ, e cảm ơn ạ
Gọi D là trung điểm AC
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AB, qua C kẻ đường thẳng vuông góc AC, chúng cắt nhau tại H
Dễ dàng nhận ra hai tam giác vuông HAC và HAB có cặp cạnh huyền - cạnh góc vuông bằng nhau nên 2 tam giác bằng nhau
\(\Rightarrow HA=HC\Rightarrow H\) nằm trên trung trực AC (do AB=BC)
\(\Rightarrow H,A,D\) thẳng hàng
\(\left\{{}\begin{matrix}CH\perp BC\\SC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SHC\right)\Rightarrow BC\perp SH\)
Tương tự ta có \(AB\perp\left(SHA\right)\Rightarrow AB\perp SH\)
\(\Rightarrow SH\perp\left(ABC\right)\)
Gọi E là trung điểm AH \(\Rightarrow ME\) là đường trung bình tam giác SAH
\(\Rightarrow ME||SH\Rightarrow ME\perp\left(ABC\right)\) đồng thời \(ME=\dfrac{1}{2}SH\)
Gọi G là trung điểm BC \(\Rightarrow AG\perp BC\), từ D kẻ \(DF\perp BC\Rightarrow DF||AG\Rightarrow DF\) là đường trung bình tam giác AGC
\(\Rightarrow DF=\dfrac{1}{2}AG=\dfrac{a\sqrt{3}}{4}\)
AGCH là hình thang (AG song song CH vì cùng vuông góc BC) \(\Rightarrow EF\) là đường trung bình hình thang
\(\Rightarrow EF\perp BC\Rightarrow E,D,F\) thẳng hàng
\(AH=\dfrac{AD}{cos\widehat{DAH}}=\dfrac{AD}{cos\widehat{ABD}}=\dfrac{AD}{cos30^0}=\dfrac{a\sqrt{3}}{3}\)
\(ED=\dfrac{1}{2}AH=\dfrac{a\sqrt{3}}{6}\) (trung tuyến tam giác vuông)
\(\Rightarrow EF=ED+DF=\dfrac{5a\sqrt{3}}{12}\)
Trong tam giác vuông MEF, từ E kẻ \(EK\perp MF\)
\(\left\{{}\begin{matrix}ME\perp\left(ABC\right)\Rightarrow ME\perp BC\\EF\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(MEF\right)\Rightarrow BC\perp EK\)
\(\Rightarrow EK\perp\left(MBC\right)\Rightarrow EK=d\left(E;\left(MBC\right)\right)\)
\(SB=2NB\Rightarrow d\left(S;\left(MBC\right)\right)=2d\left(N;\left(MBC\right)\right)\)
\(SM=AM\Rightarrow d\left(S;\left(MBC\right)\right)=d\left(A;\left(MBC\right)\right)\)
\(AC=2DC\Rightarrow d\left(A;\left(MBC\right)\right)=2d\left(D;\left(MBC\right)\right)\)
\(\dfrac{EF}{DF}=\dfrac{5}{3}\Rightarrow d\left(E;\left(MBC\right)\right)=\dfrac{5}{3}d\left(D;\left(MBC\right)\right)=\dfrac{5}{3}d\left(N;\left(MBC\right)\right)\)
\(\Rightarrow EK=\dfrac{5}{3}.\dfrac{3a}{7}=\dfrac{5a}{7}\)
\(\dfrac{1}{EK^2}=\dfrac{1}{ME^2}+\dfrac{1}{EF^2}\Rightarrow ME=\dfrac{EF.EK}{\sqrt{EF^2-EK^2}}=5a\)
\(\Rightarrow SH=2ME=10a\)
\(V=\dfrac{1}{3}.10a.\dfrac{a^2\sqrt{3}}{4}=\dfrac{5a^3\sqrt{3}}{6}\)
Đúng 1
Bình luận (0)