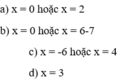bạn tách từng bài ra bn

tl câu hỏi trên cho mik ik

a) 2x² - 3x - 2 = 0.

<=> (2x + 1)(x - 2) = 0

<=> 2x + 1 = 0 hoặc x - 2 = 0

<=> x = -1/2 hoặc x = 2

b) 3x² - 7x - 10 = 0.

<=> (x + 1)(3x - 10) = 0

<=> x = -1 hoặc x = 10/3

c) 2x² - 5x + 3 = 0.

<=> (x - 1)(2x - 3) = 0

<=> x = 1 hoặc x = 3/2

a) \(\left(x^2-3x\right)\left(x^2+7x+10\right)=216\Rightarrow x\left(x-3\right)\left(x+2\right)\left(x+5\right)=216\)

\(\Rightarrow x\left(x+2\right)\left(x-3\right)\left(x+5\right)=216\Rightarrow\left(x^2+2x\right)\left(x^2+2x-15\right)=216\)

Đặt \(t=x^2+2x\Rightarrow\) pt trở thành \(t\left(t-15\right)=216\Rightarrow t^2-15t-216=0\)

\(\Rightarrow\left(t+9\right)\left(t-24\right)=0\Rightarrow\left[{}\begin{matrix}t=-9\\t=24\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x^2+2x=-9\\x^2+2x=24\end{matrix}\right.\)

\(TH_1:x^2+2x=-9\Rightarrow x^2+2x+9=0\Rightarrow\left(x+1\right)^2+8=0\) (vô lý)

\(TH_2:x^2+2x=24\Rightarrow x^2+2x-24=0\Rightarrow\left(x-4\right)\left(x+6\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-6\end{matrix}\right.\)

b) \(\left(2x^2-7x+3\right)\left(2x^2+x-3\right)+9=0\)

\(\Rightarrow\left(x-3\right)\left(2x-1\right)\left(x-1\right)\left(2x+3\right)+9=0\)

\(\Rightarrow\left(x-3\right)\left(2x+3\right)\left(x-1\right)\left(2x-1\right)+9=0\)

\(\Rightarrow\left(2x^2-3x-9\right)\left(2x^2-3x+1\right)+9=0\)

Đặt \(t=2x^2-3x-9\Rightarrow\) pt trở thành \(t\left(t+10\right)+9=0\)

\(\Rightarrow t^2+10t+9=0\Rightarrow\left(t+1\right)\left(t+9\right)=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-9\end{matrix}\right.\)

\(TH_1:t=-1\Rightarrow2x^2-3x-9=-1\Rightarrow2x^2-3x-8=0\)

\(\Delta=\left(-3\right)^2-4\left(-8\right).2=73\Rightarrow\left[{}\begin{matrix}x=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3-\sqrt{73}}{4}\\x=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3+\sqrt{73}}{4}\end{matrix}\right.\)

\(TH_2:t=-9\Rightarrow2x^2-3x-9=-9\Rightarrow2x^2-3x=0\Rightarrow x\left(2x-3\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)

\(2x^2+5x+3=0\)

\(\Leftrightarrow2x^2+2x+3x+3=0\)

\(\Leftrightarrow2x\left(x+1\right)+3\left(x+1\right)=0\)

\(\Leftrightarrow\left(2x+3\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+3=0\\x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=-1\end{matrix}\right.\)

Vậy \(S=\left\{-1;-\dfrac{3}{2}\right\}\)

\(\left(x-\sqrt{2}\right)-3\left(x^2-2\right)=0\)

\(\Leftrightarrow x-\sqrt{2}-3x^2+6=0\)

\(\Leftrightarrow-3x^2+x+6-\sqrt{2}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{1}{6}-\dfrac{\sqrt{73-3\sqrt{32}}}{6}\\x_2=\dfrac{\sqrt{73-3\sqrt{32}}}{6}+\dfrac{1}{6}\end{matrix}\right.\)

1.

a) \(2x^4-4x^3+2x^2\)

\(=2x^2\left(x^2-2x+1\right)\)

\(=2x^2\left(x-1\right)^2\)

b) \(2x^2-2xy+5x-5y\)

\(=\left(2x^2-2xy\right)+\left(5x-5y\right)\)

\(=2x\left(x-y\right)+5\left(x-y\right)\)

\(=\left(x-y\right)\cdot\left(2x+5\right)\)

2 . 

a,

\(4x\left(x-3\right)-x+3=0\)

⇒\(4x\left(x-3\right)-\left(x-3\right)=0\)

⇒\(\left(x-3\right)\left(4x-1\right)=0\)

⇒\(\left[{}\begin{matrix}x-3=0\\4x-1=0\end{matrix}\right.\)

⇔\(\left[{}\begin{matrix}x=3\\4x=1\end{matrix}\right.\)

⇔\(\left[{}\begin{matrix}x=3\\x=\dfrac{1}{4}\end{matrix}\right.\)

vậy \(x\in\left\{3;\dfrac{1}{4}\right\}\)

b, 

\(\)\(\left(2x-3\right)^2-\left(x+1\right)^2=0\)

⇒\(\left(2x-3-x-1\right)\left(2x-3+x+1\right)\) = 0

⇒\(\left(x-4\right)\left(3x-2\right)=0\)

⇔\(\left[{}\begin{matrix}x-4=0\\3x-2=0\end{matrix}\right.\)

⇔\(\left[{}\begin{matrix}x=4\\3x=2\end{matrix}\right.\)

⇔\(\left[{}\begin{matrix}x=4\\x=\dfrac{2}{3}\end{matrix}\right.\)

vậy \(x\in\left\{4;\dfrac{2}{3}\right\}\)

ban tích cho mk vs nha

B = {3/2;1}

a, 12 - (2\(x^2\) - 3) = 7

            2\(x^2\)  - 3  =  12  - 7

           2\(x^2\) - 3  = 5

           2\(x^2\)  = 8

             \(x^2\)   = 4

             \(\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)

a) \(12-\left(2x^2-3\right)=7\\ 12-2x^2+3=7\\ 15-2x^2=7\\ 2x^2=15-7=8\\ x^2=8:2=4\\ x=\pm2\)

b) \(3x^2-12=2x^2+4\\ 3x^2-2x^2=12+4\\ x^2=16\\ x=\pm4\)

b, 3\(x^2\) - 12  = 2\(x^2\) + 4

    3\(x^2\) - 2\(x^2\) = 12 + 4

     \(x^2\) = 16

      \(\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)