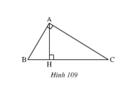
Cho tam giác ABC có = 900, kẻ AH vuông góc với BC(H∈BC). C ác tam giác AHC và BAC có AC là cạnh chung, là góc chung,
=
=900,
nhưng hai tam giác không bằng nhau. Tại sao ở đây không áp dụng trường hợp góc cạnh góc để kết luận
∆AHC= ∆BAC?
Cho tam giác ABC có góc A = 90o. Kẻ AH vuông góc với BC. Các tam giác AHC và BAC có AC cạnh chung, góc C là góc chung, góc AHC = góc BHC = 90o nhưng hai tam giác này không bằng nhau.
Tại sao ở đây không thể áp dụng trường hợp góc - cạnh góc để kết luận tam giác AHC = tam giác BAC
Hai tam giác AHC và BAC có:
Nhưng hai tam giác này không bằng nhau vì góc AHC không phải là góc kề với cạnh AC
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC(H thuộc BC). Các tam giác AHC và BAC có AC là cạnh chung, góc C là góc chung, góc AHC = góc BAC = 90 độ nhưng 2 tam giác đó không bằng nhau. Tại sao ở đây không thể áp dụng các trường hợp góc - cạnh - góc để kết luận TG AHC = TG BAC?
cho tam giác ABC vuông tại A. kẻ AH vuông góc với BC (H tuộc BC). Các tam giác ahc VÀ bac CÓ ac LÀ CẠNH CHUNG. tẠI SAO Ở ĐÂY KHÔNG THỂ ÁP DỤNG CÁC TRƯỜNG HỢP GÓC-CẠNH-GÓC để kết luận tam giác AHC = tam giác BAC
Vì AH ko bằng cạnh AB và HC ko bằng cạnh BC nên ta ko thể kết luận tam giác AHC = tam giác BAC theo trường hợp cạnh - cạnh - cạnh
Xét hai tam giác ΔAHC và ΔBAC có:
-AC chung
-Góc BAC = góc AHC
=>Ko đủ dữ kiện để kết luận hai tam giác trên bằng nhau
Xét tam giác AHC và BAC có:
AC là cạnh chung
AHC =BAC= 90*
C là góc chung
Nhưng 2 tam giác này k = nhau
Do AHC k kề với AC
cho tam giác ABC có A=90 độ
kẻ AH vuông góc với BC (H thuộc BC)
các tam giác AHC và BAC có AC chung, C là góc chung, góc AHC=BAC=90 độ nhưng tam giác đó k bằng nhau, tại sao ko thể áp dụng TH góc cạnh góc để KL 2 tam giác = nhau
Cho tam giác ABC có \(\widehat{A}=90^0\) (h.109). Kẻ AH vuông góc với BC (\(H\in BC\) ). Các tam giác AHC và BAC có AC là cạnh chung. \(\widehat{C}\) là góc chung, \(\widehat{AHC}=\widehat{BAC}=90^0\), nhưng hai tam giác đó không bằng nhau
Tại sao ở đây không thể áp dụng trường hợp góc - cạnh - góc để kết luận \(\Delta AHC=\Delta BAC\) ?

vì cạnh của hai tam giác không xen giữa 2 góc
trên hình vẽ, các tam giác ABC và A'BC có cạnh chung BC = 30cm, CA = CA' = 2 cm, góc ABC= góc A'BC =30 độ nhưng hai tam giác dó không bằng nhau
Tại sao ở đây không thể áp dụng trường hợp cạnh - góc - cạnh để kết luận tam giác ABC = tam giác A'BC ?
Trên hình 90, các tam giác ABC và A'BC có cạnh chung BC = 3cm, CA = CA’ = 2cm, A B C ^ = A ' B C ^ = 30 o nhưng hai tam giác đó không bằng nhau.
Tại sao ở đây không thể áp dụng trường hợp c-g-c để kết luận
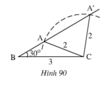
Góc ABC không phải là góc xen giữa hai cạnh BC và CA góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh - góc - cạnh để kết luận hai tam giác bằng nhau.
Chọn câu đúng nhất.1 .Cho ∆ ABC vuông cân tại A. vậy góc B bằng:A. 600B. 900C. 450D. 12002. Một tam giác là vuông nếu độ dài 3 cạnh của nó là:A. 2,3,4 B. 3,4,5 C. 4,5,6 D. 6,7,83. Một tam giác cân có góc ở đáy là 350 thì góc ở đỉnh có số đo là:A. 1000B. 1100C. 850D. 12004. Tam giác ABC có BC = 3cm ; AC = 5cm ; AB = 4cm. Tam giác ABC vuông tại đâu?A. Tại B B. Tại C C. Tại A D. Không phải là tam giác vuông5. Tam giác ABC có AB = AC = BC thì tam giác ABC là A. Tam giác nhọn B. Tam giác cân C. Tam giác vuông D. Tam giác đều6. Tam giác nào vuông nếu độ lớn ba góc kà:A. 300, 700, 800B. 200, 700, 900 C. 650, 450, 700D. 600, 600, 6007. Tam giác cân là tam giác có:A. Hai cạnh bằng nhau -B. Ba cạnh bằng nhau - C. Một góc bằng 600 - D. Một góc bằng 900
Cho tam giác ABC cân tại A, có 𝐵𝐴𝐶 = 700 . Vẽ AH vuông góc với BC. a) Chứng minh tam giác AHB = tam giác AHC và AH là tia phân giác của góc BAC. b) So sánh độ dài cạnh AH và BH. c) Từ H vẽ HD vuông góc AB và HE vuông góc AC . Tam giác ADE là tam giác gì ? Vì sao? d) Qua D vẽ đường thẳng DK vuông góc với BC tại K. Chứng minh DK < KE
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc BAC
b: \(\widehat{BAC}=70^0\)
nên \(\widehat{BAH}=35^0\)
=>\(\widehat{B}=55^0\)
=>BH<AH
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: AD=AE
hay ΔADE cân tại A
Cho tam giác ABC có AB=AC=10cm, BC= 12 . Vẽ AH vuông góc với BC tại H.
a, CMR: tam giác ABC cân
b, Chứng minh tam giác AHB = tam giác AHC. Từ đó chứng minh AH là phân giác của góc A
c, Từ H vẽ HN vuông góc với Ab và kẻ HN vuông góc với Ac. CMR : tam giác BHM = tam giác CHN
e, Tính độ dài AH
f, Từ B kẻ Bx vuông góc với AB, từ C kẻ Cy vuông góc với AC, chúng cắt nhau tại O. Tam giác OBC là tam giác gì ? Vì sao ?
a) Vì AB = AC =10cm => (đpcm)
b) Xét \(\Delta AHB\)và \(\Delta AHC\)có;
AB = AC(gt)
\(\widehat{AHB}=\widehat{AHC}=90^o\)
AH chung
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.g.c\right)\)
\(\Rightarrow HB=HC\)(2 cạnh tương ứng)(1)
\(\Rightarrow\widehat{B}=\widehat{C}\)(2 góc tương ứng)(2)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\Rightarrow\)AH là tia phân giác của \(\widehat{A}\)
c) HM với HN?
Vì \(\Delta HMB;\Delta HNC\)là tam giác vuông nên từ (1);(2) =>\(\Delta HMB=\Delta HNC\)
e)Xét \(\Delta AHC\)vuông:
Áp dụng định lí Py ta go ta có:
\(AC^2=CH^2+AH^2\)
\(12^2=6^2+AH^2\)
\(\Rightarrow AH^2=12^2-6^2=144-36=108\)
\(\Rightarrow AH=\sqrt{108}cm\)
Thông cảm nhé tối qua mình tắt mất nên nay làm tiếp:D
Vì \(\widehat{ABO}=\widehat{ACO}=90^o\)mà \(\widehat{ABC}=\widehat{ACB}=60^o\Rightarrow\widehat{BCO}=\widehat{CBO}=30^o\)
Do \(\widehat{BCO}=\widehat{CBO}=30^o\)nên \(\Delta OBC\)là tam giác cân