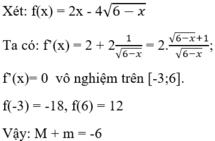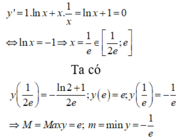tìm giá trị lớn nhất và giá trị nhỏ nhất của M = ab/a+b

Những câu hỏi liên quan
Bài 5 : Cho a và b là các số nguyên có 2 chữ số . Hãy tìm giá trị lớn nhất và giá trị nhỏ nhất của tổng a + b ?
số lớn nhất có 2 cs là 99 thì a+b=9+9=18
số bé nhất có 2 cs là -99 thì a+b=(-9)+(-9)=-18
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P=x+\sqrt{4-x^2}\)
TXĐ: D=[-2,2]
P'=\(1-\frac{x}{\sqrt{4-x^2}}\)
P'=0<=> \(1-\frac{x}{\sqrt{4-x^2}}=0\)=>\(\hept{\begin{cases}x=\sqrt{4-x^2}\\4-x^2>0\end{cases}}\)
\(\hept{\begin{cases}x^2=4-x^2\\x\ge0\\-2< x< 2\end{cases}}\)
=> \(x=\sqrt{2}\)
P(-2)=-2
\(P\left(\sqrt{2}\right)=2\sqrt{2}\)
P(2)=2
Vậy GTLN của P=\(2\sqrt{2}\),GTNN là -2
Đúng 0
Bình luận (0)
Cho x ,y thuộc Z:
a, Với giá trị nào của x thì A = 100 - |x + 5| có giá trị lớn nhất . Tìm giá trị đó.
b, Với giá trị nào của y thì B = |y - 3| + 50 có giá trị nhỏ nhất. Tìm giá trị đó
a) Vì \(\left|x-5\right|\ge0\)nên \(100-\left|x-5\right|\le100\)
Để A lớn nhất thì \(\left|x-5\right|=0\Leftrightarrow x=-5\)
Vậy A lớn nhất bằng 100 khi và chỉ khi x= -5
b) Vì \(\left|y-3\right|\ge0\)nên \(\left|y-3\right|+50\ge50\)
Để B lớn nhất thì \(\left|y-3\right|=0\Leftrightarrow y=3\)
Vậy B nhỏ nhất bằng 50 khi và chỉ khi y= 3
Tập hợp các số tự nhiên n bằng ( 0 1 2 3 4...)
Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của các biểu thức sau 
\(\dfrac{3x^2-1}{x^2+2}=\dfrac{6x^2-2}{2\left(x^2+2\right)}=\dfrac{7x^2-\left(x^2+2\right)}{2\left(x^2+2\right)}=\dfrac{7x^2}{2\left(x^2+2\right)}-\dfrac{1}{2}\ge=-\dfrac{1}{2}\)
GTNN của biểu thức là \(-\dfrac{1}{2}\), xảy ra khi \(x=0\)
Biểu thức ko tồn tại GTLN
Đúng 4
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
A = a + b + c + ab + bc + ca , với a, b, c thuộc R
thỏa mãn: a^2 +b^2 +c^2 =3.
\(A=a+b+c+\dfrac{\left(a+b+c\right)^2-\left(a^2+b^2+c^2\right)}{2}=\dfrac{1}{2}\left(a+b+c\right)^2+\left(a+b+c\right)-\dfrac{3}{2}\)
\(A=\dfrac{1}{2}\left(a+b+c+1\right)^2-2\ge-2\)
\(A_{min}=-2\) khi \(a+b+c=-1\) (có vô số bộ a;b;c thỏa mãn điều này)
Với mọi a;b;c ta luôn có:
\(\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2+\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)+3\ge2\left(a+b+c+ab+bc+ca\right)\)
\(\Leftrightarrow12\ge2A\)
\(\Rightarrow A\le6\)
\(A_{max}=6\) khi \(a=b=c=1\)
Đúng 2
Bình luận (0)
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f
(
x
)
2
x
-
4
6
-
x
trên đoạn [-3;6]. Tổng M + m có giá trị là A. 18 B. -6 C. -12 D. -4
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = 2 x - 4 6 - x trên đoạn [-3;6]. Tổng M + m có giá trị là
A. 18
B. -6
C. -12
D. -4
cho −5 ≤ x ≤ 12 và −112≤ y ≤157
tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hiệu x-y
cách giải nha
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
y
xlnx
trên đoạn
1
2
e
;
e
lần lượt là A.
M
e
,
m
-
1
2
e
ln...
Đọc tiếp
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = xlnx trên đoạn 1 2 e ; e lần lượt là
A. M = e , m = - 1 2 e ln 2 e
B. M = e , m = - 1 2 e
C. M = - 1 2 e ln 2 e , m = - e - 1
D. M = e , m = - 1 e
cho bốn đường thẳng cắt nhau đôi một , tạo thành m giao điểm
a,Tìm giá trị nhỏ nhất của m
b,Tìm giá trị lớn nhất của m