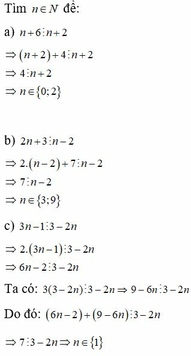( n^2 +3n +6 )) ⋮ ( n + 3 )

Những câu hỏi liên quan
Chứng minh rằng
a) A = n(3n-1) - 3n(n-2) ⋮ 5 (∀n ϵ R)
b) B = n(n+5) - (n-3)(n+2) ⋮ 6 (∀n ∈ Z)
c) C= (n2 + 3n - 1)(n+2) - n3+2 ⋮ 5 (∀n ϵ Z)
a: A=3n^2-n-3n^2+6n=5n chia hết cho 5
b: B=n^2+5n-n^2+n+6=6n+6=6(n+1) chia hết cho 6
c: =n^3+2n^2+3n^2+6n-n-2-n^3+2
=5n^2+5n
=5(n^2+n) chia hết cho 5
Đúng 0
Bình luận (0)
cho mọi số nguyên dương n>2 cmr \(\dfrac{1}{3}\)\(\dfrac{ }{ }\). \(\dfrac{4}{6}.\dfrac{7}{9}.\dfrac{10}{12}........\dfrac{3n-2}{3n}.\dfrac{3n+1}{3n+3}< \dfrac{1}{3\sqrt{n+1}}\)
chứng minh rằng với n nguyên thì n^6 + n^4 - 3n^3 +7n^2 -3n + 3 ko là số chính phương
Bài 6: Tìm giá trị nguyên của n để :
1) 3n^3 +10n^2 - 5 chia hết cho 3n+1
2) 4n^3 +11n^2 +5n+ 5 chia hết cho n+2
3) n^3 - 4n^2 +5n -1 chia hết cho n-3
1: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;4;2;-2;-1;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;3;-3\right\}\)
hay \(n\in\left\{0;1;-1\right\}\)
Đúng 0
Bình luận (0)
Tìm
n
∈
N
để:a)
n
+
6
⋮
n
+
2
b)
2
n
+
3
⋮
n
-
2
c)
3
n
-
1
⋮
3
-
2
n
Đọc tiếp
Tìm n ∈ N để:
a) n + 6 ⋮ n + 2
b) 2 n + 3 ⋮ n - 2
c) 3 n - 1 ⋮ 3 - 2 n
Tìm n ∈ N để:
a, n+6 ⋮ n+2
b, 2n+3 ⋮ n - 2
c, 3n - 1 ⋮ 3 - 2n
a, n+6 ⋮ n+2 => (n+2)+4 ⋮ n+2
=> 4 ⋮ n+2
=> n ∈ {0;2}
b, 2n+3 ⋮ n - 2
=> 2.(n - 2)+7 ⋮ n - 2
=> 7 ⋮ n - 2
=> n ∈ {3;9}
c, 3n - 1 ⋮ 3 - 2n
=> 2.(3n - 1) ⋮ 3 - 2n
=> 6n - 2 ⋮ 3 - 2n
Ta có: 3(3 - 2n) ⋮ 3 - 2n => 9 - 6n ⋮ 3 - 2n
Do đó: (6n - 2)+(9 - 6n) ⋮ 3 - 2n
=> 7 ⋮ 3 - 2n => n ∈ {1}
Đúng 0
Bình luận (0)
chứng minh rằng với n là số nguyên thì n^6+n^4-3n^3+7n^2-3n+3 không là số chính phương
hello l am Duong quang minh, nice to meet you, how old are you, l am nine how do you spell your name ,m-i-n-h
Tìm n thuộc N:
1) 3n + 5 chia hết cho n - 4
2) 6n + 7 chia hết cho 3n - 1
3) 4n + 8 chia hết cho 3n - 2
4) 2n - 7 chia hết cho n + 2
5) 3n - 4 chia hết cho 3 - n
6) 2n - 5 chia hết cho n + 1
7) 3n - 7 chia hết cho 2n + 3
8) n - 5 chia hết cho n - 1
1: =>3n-12+17 chia hết cho n-4
=>\(n-4\in\left\{1;-1;17;-17\right\}\)
hay \(n\in\left\{5;3;21;-13\right\}\)
2: =>6n-2+9 chia hết cho 3n-1
=>\(3n-1\in\left\{1;-1;3;-3;9;-9\right\}\)
hay \(n\in\left\{\dfrac{2}{3};0;\dfrac{4}{3};-\dfrac{2}{3};\dfrac{10}{3};-\dfrac{8}{3}\right\}\)
4: =>2n+4-11 chia hết cho n+2
=>\(n+2\in\left\{1;-1;11;-11\right\}\)
hay \(n\in\left\{-1;-3;9;-13\right\}\)
5: =>3n-4 chia hết cho n-3
=>3n-9+5 chia hết cho n-3
=>\(n-3\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{4;2;8;-2\right\}\)
6: =>2n+2-7 chia hết cho n+1
=>\(n+1\in\left\{1;-1;7;-7\right\}\)
hay \(n\in\left\{0;-2;6;-8\right\}\)
Đúng 0
Bình luận (0)
n^3-n chia hết cho 6
n^3-13n chia hết cho 6
2n^3+3n^2+n chia hết cho 6
n^3-n= n( n^2-1) = n(n+1)(n-1) chia hết cho 6
các câu khác tg tự
Đúng 0
Bình luận (0)
n3 - 13n = n(n2 - 13)
* chứng minh nó chia hết cho 2
Với n chẵn thì n chia hết cho 2 => n3 - 13n chia hết cho 2
Với n lẻ thì (n2 - 13) chia hết cho 2 => n3 - 13n chia hết cho 2
* chứng minh nó chia hết cho 3
Với n = 3k thì nó chia hết cho 3
Với n = 3k + 1 thì n2 - 13 = 9k2 + 6k - 12 chia hết cho 3 => nó chia hết cho 3
Với n = 3k + 2 thì n2 - 13 = 9k2 + 12k - 9 chia hết cho 3 => nó chia hết cho 3
Từ đây ta có n3 - 13n chia hết cho 6
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm x:
a, (n^2 + 3n + 1) ⋮ (n + 1)
b, (6n + 7) ⋮ (3n - 2)
c, (n^2 + 3n + 6) ⋮ (n + 3)