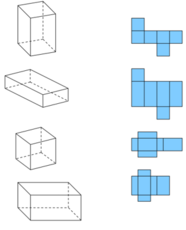
Mảnh bìa nào dưới đây có thể gấp được thành một hình lập phương?

Những câu hỏi liên quan
Mảnh bìa nào dưới đây có thể ghép được thành một hình lập phương
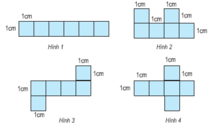
Cách 1: học sinh vẽ hình lên giấy rồi gấp thử và trả lời
Cách 2: suy luận:
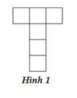
-đương nhiên là không thể gấp hình 1 thành một hình lập phương.
- Với hình 2, khi ta gấp dãy 4 hình vuông ở dưới thành 4 mặt xung quanh thì 2 hình vuông ở trên sẽ đè lên nhau, không tạo thành một mặt đáy trên và một mặt đáy dưới được. Do đó hình 2 cũng bị loại.
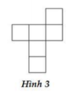
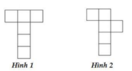
- Hình 3 và hình 4 đều có thể gấp thành hình lập phương vì khi ta gấp dãy 4 hình vuông ở giữa thành 4 mặt xung quanh thì 2 hình vuông trên và dưới sẽ tạo thành hai mặt đáy trên và đáy dưới
Mỗi mảnh bìa ở hình 3 và hình 4 đều có thể gấp thành một hình lập phương.
Nói thêm :
a) Mọi mảnh bìa (6 hình vuông bằng nhau) gồm có một dãy 4 hình vuông ở giữa, 1 hình vuông ở phía trên, 1 hình vuông ở phía dưới đều có thể gấp lại thành một hình lập phương.
Ví dụ, các mảnh bìa sau có thể gấp được thành hình lập phương:
b) Mọi mảnh bìa gồm 6 hình vuông bằng nhau nhưng không có dạng đã nêu ở (a) thì không thể gấp lại thành hình lập phương được.
Đúng 0
Bình luận (0)
Mảnh bìa nào dưới đây có thể ghép được thành một hình lập phương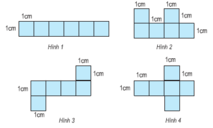
Cách 1: học sinh vẽ hình lên giấy rồi gấp thử và trả lời
Cách 2: suy luận:
-đương nhiên là không thể gấp hình 1 thành một hình lập phương.
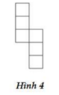
- Với hình 2, khi ta gấp dãy 4 hình vuông ở dưới thành 4 mặt xung quanh thì 2 hình vuông ở trên sẽ đè lên nhau, không tạo thành một mặt đáy trên và một mặt đáy dưới được. Do đó hình 2 cũng bị loại.
- Hình 3 và hình 4 đều có thể gấp thành hình lập phương vì khi ta gấp dãy 4 hình vuông ở giữa thành 4 mặt xung quanh thì 2 hình vuông trên và dưới sẽ tạo thành hai mặt đáy trên và đáy dưới
Mỗi mảnh bìa ở hình 3 và hình 4 đều có thể gấp thành một hình lập phương.
Nói thêm :
a) Mọi mảnh bìa (6 hình vuông bằng nhau) gồm có một dãy 4 hình vuông ở giữa, 1 hình vuông ở phía trên, 1 hình vuông ở phía dưới đều có thể gấp lại thành một hình lập phương.
Ví dụ, các mảnh bìa sau có thể gấp được thành hình lập phương:
b) Mọi mảnh bìa gồm 6 hình vuông bằng nhau nhưng không có dạng đã nêu ở (a) thì không thể gấp lại thành hình lập phương được.
Đúng 0
Bình luận (0)
Nối mảnh bìa có thể gấp được thành hình hộp chữ nhật hoặc hình lập phương cho thích hợp :
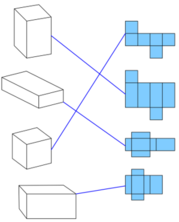
Tấm bìa cạnh bên được gấp lại thành một hình lập phương.Hỏi:
a)Hình lập phương này có mặt với D là mặt nào trong các mặt a,b,c,d,e,f ?
b) Thể tích hình lập phương nêu trên có bao nhiêu m3 ? Dm3
Lan có một tấm bìa có kích thước như hình vẽ:

Lan có thể gấp tấm bìa thành một hình lập phương. Đúng hay sai?
A. Đúng
B. Sai
Có thể vẽ hình lên giấy rồi gấp thử ta thấy không thể gấp mảnh bìa đã cho thành một hình lập phương.
Vậy đáp án đúng là "Sai".
Đáp án B
Đúng 0
Bình luận (0)
có 1000 mảnh bìa hình chữ nhật ,trên mỗi mảnh bìa được ghi các số từ 2 đến 1001 sao cho không có hai mảnh nào ghi số giống nhau .Chứng minh rằng không thể ghép các mảnh bìa này liền nhau để được một số chính phương
mình cần gấp
Giờ ta phải chứng minh cho 1 số chính phương chia cho 3 chỉ dư 0 hoặc 1
Với số tự nhiên a có dạng a=3k±1
=> a²=(3k±1)²=9k²±6k+1 chia cho 3 dư 1
Với a⁞3 thì chắc chắn a² chia cho 3 dư 0 rồi.
Xong.
Việc còn lại của bạn bây giờ quá đơn giản, chứng minh cho số đó chia cho 3 dư 2.
Nếu 1000 mảnh bìa đó xếp thành 1 số thì nó se có tổng các chữ số là:
(2+1001)x1000/2 = 501500 chia cho 3 dư 2. Vậy số ta vừa ghép được chia cho 3 dư 2.
=> số đó không phải số chính phương.
Đúng 0
Bình luận (0)
Có bao nhiêu lưới đa giác trong số các lưới dưới đây có thể gấp lại tạo thành mô hình một khối lập phương? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Có bao nhiêu lưới đa giác trong số các lưới dưới đây có thể gấp lại tạo thành mô hình một khối lập phương?

A. 1
B. 2
C. 3
D. 4
Đáp án D
Cả 4 hình trên đều lắp ghép ra được khối lập phương.
Đúng 0
Bình luận (0)
Có bao nhiêu lưới đa giác trong số các lưới dưới đây có thể gấp lại tạo thành mô hình một khối lập phương?

A. 1
B. 2
C. 3
D. 4
Đáp án D
Cả 4 hình trên đều lắp ghép ra được khối lập phương.
Đúng 0
Bình luận (0)
Có 1000 mảnh bìa hình chữ nhật, trên mỗi mảnh được ghi một trong các số từ 1 đến 1001 (không có mảnh nào ghi khác nhau). Chứng minh rằng không thể ghép tất cả các mảnh bìa đó liền nhau để được một số chính phương.
Giờ ta phải chứng minh cho 1 số chính phương chia cho 3 chỉ dư 0 hoặc 1
Với số tự nhiên a có dạng a=3k±1
=> a²=(3k±1)²=9k²±6k+1 chia cho 3 dư 1
Với a⁞3 thì chắc chắn a² chia cho 3 dư 0 rồi.
Xong.
Việc còn lại của bạn bây giờ quá đơn giản, chứng minh cho số đó chia cho 3 dư 2.
Nếu 1000 mảnh bìa đó xếp thành 1 số thì nó se có tổng các chữ số là:
(2+1001)x1000/2 = 501500 chia cho 3 dư 2. Vậy số ta vừa ghép được chia cho 3 dư 2.
=> số đó không phải số chính phương.
Đúng 0
Bình luận (0)
Giờ ta phải chứng minh cho 1 số chính phương chia cho 3 chỉ dư 0 hoặc 1
Với số tự nhiên a có dạng a=3k±1
=> a²=(3k±1)²=9k²±6k+1 chia cho 3 dư 1
Với a⁞3 thì chắc chắn a² chia cho 3 dư 0 rồi.
Xong.
Việc còn lại của bạn bây giờ quá đơn giản, chứng minh cho số đó chia cho 3 dư 2.
Nếu 1000 mảnh bìa đó xếp thành 1 số thì nó se có tổng các chữ số là:
(2+1001)x1000/2 = 501500 chia cho 3 dư 2. Vậy số ta vừa ghép được chia cho 3 dư 2.
=> số đó không phải số chính phương
k cho mk nha @@
Đúng 0
Bình luận (0)
Xem thêm câu trả lời