Xác định độ dài trục lớn, trục nhỏ, tiêu cự, tâm sai, tiêu điểm, đỉnh, đường chuẩn của elip:
\(\left(E\right):4x^2+9y^2-36=0\)
Giúp cần gấp
Ta có: \(\left(E\right):4x^2+9y^2=36\Leftrightarrow\frac{x^2}{9}+\frac{y^2}{4}=1\)
\(a^2=9\Rightarrow a=3\)
\(b^2=4\Rightarrow b=2\)
\(c^2=a^2-b^2=9-4=5\Rightarrow c=\sqrt{5}\)
Tọa độ các đỉnh: \(A_1\left(-3;0\right),A_2\left(3;0,\right),B_1\left(0;-2\right),B_2\left(0;2\right)\)
Tọa độ các tiêu điểm: \(F_1\left(-\sqrt{5};0\right),F_2\left(\sqrt{5};0\right)\)
Độ dài trục lớn \(A_1A_2\div2a=6\)
Độ dài trục nhỏ \(B_1B_2\div2b=4\)
Tiêu cự: \(2c=2\sqrt{5}\)
Tâm sai: \(e=\frac{c}{a}=\frac{\sqrt{5}}{3}\)
Đường chuẩn: \(x=\pm\frac{a^2}{c}=\pm\frac{9}{\sqrt{5}}\)
Đúng 0
Bình luận (2)
Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip (E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6. Phương trình nào sau đây là phương trình của elip (E). A.
x
2
25
+
y
2
16
1
B.
x
2
16
+
y
2...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip (E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6. Phương trình nào sau đây là phương trình của elip (E).
A. x 2 25 + y 2 16 = 1
B. x 2 16 + y 2 25 = 1
C. x 2 36 + y 2 9 = 1
D. x 2 9 + y 2 36 = 1
Chọn A.
Độ dài trục lớn bằng 10 ⇒ 2a = 10 ⇔ a = 5, a 2 = 25
Độ dài tiêu cự bằng 6 ⇒ 2c = 6 ⇔ c = 3
Ta có: a 2 - b 2 = c 2 ⇒ b 2 = a 2 - c 2 = 5 2 - 3 2 = 16
Vậy phương trình của elip (E) là:
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip ( E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6 . Phương trình nào sau đây là phương trình của elip (E). A.
x
2
25
+
y
2
16
1
B.
x
2
16
+...
Đọc tiếp
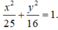
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip ( E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6 . Phương
trình nào sau đây là phương trình của elip (E).
A. x 2 25 + y 2 16 = 1
B. x 2 16 + y 2 25 = 1
C. x 2 36 + y 2 9 = 1
D. x 2 144 + y 2 36 = 0
Ta có: độ dài trục lớn là 10 nên 2a= 10 => a= 5.
Độ dài tiêu cự là 6 nên 2c= 6 => c= 3
Ta có: b2 = a2- c2= 25- 9= 16 => b= 4
Vậy phương trình của Elip là: x 2 25 + y 2 16 = 1
Chọn A.
Đúng 0
Bình luận (0)
Cho elip (E) : \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\left(0< b< a\right)\). Tính tỉ số \(\dfrac{c}{a}\) trong các trường hợp sau :
a) Trục lớn bằng ba lần trục nhỏ
b) Đỉnh trên trục nhỏ nhìn hai tiêu điểm dưới một góc vuông
c) Khoảng cách giữa đỉnh trên trục nhỏ và đỉnh trên trục lớn bằng tiêu cự
Cho elip (E) có độ dài trục lớn gấp hai lần độ dài trục nhỏ và tiêu cự bằng 6. Viết phương trình của (E)? A.
x
2
12
-
y
2
3
1
B.
x
2
12
+
y
2...
Đọc tiếp
Cho elip (E) có độ dài trục lớn gấp hai lần độ dài trục nhỏ và tiêu cự bằng 6. Viết phương trình của (E)?
A. x 2 12 - y 2 3 = 1
B. x 2 12 + y 2 3 = 1
C. x 2 3 + y 2 12 = 1
D. x 2 48 + y 2 12 = 1
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip (E) có độ dài trục nhỏ bằng 8 và độ dài tiêu cự bằng 10 Phương trình nào sau đây là phương trình của elip (E) A.
x
2
25
+
y
2
16
1
B.
x
2
16
+...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip (E) có độ dài trục nhỏ bằng 8 và độ dài tiêu cự bằng 10 Phương
trình nào sau đây là phương trình của elip (E)
A. x 2 25 + y 2 16 = 1
B. x 2 16 + y 2 41 = 1
C. x 2 36 + y 2 9 = 1
D. x 2 41 + y 2 16 = 1
Ta có: độ dài trục nhỏ là 8 nên 2b = 8 => b= 4.
Độ dài tiêu cự là 10 nên 2c = 10 => c= 5.
Lại có : a2= b2+ c2= 16+ 25= 41
Vậy phương trình của Elip là: x 2 41 + y 2 16 = 1
Chọn D.
Đúng 0
Bình luận (0)
Cho elip $\left( E \right): \, \dfrac{{ x^2}}{36}+\dfrac{{{y}^2}}{25}=1$. Xác định tiêu điểm, tiêu cự, trục lớn, trục bé, tâm sai của elip đó.
Có \(c=\sqrt{a^2-b^2}=\sqrt{11}\)
Tiêu điểm \(F_1\left(\sqrt{11},0\right);F_2\left(-\sqrt{11},0\right)\)
Tiêu cự \(F_1F_2=2\sqrt{11}\)
Trục lớn : 2a = 12
Trục bé 2b = 10
Tâm sai \(e=\dfrac{c}{a}=\dfrac{\sqrt{11}}{6}\)
Đúng 1
Bình luận (0)
a) Viết phương trình chính tắc của elip (E) đi qua điểm \(A\left(0;2\right)\) và có một tiêu điểm là \(F_1\left(-\sqrt{5};0\right)\)
b) Tìm độ dài trục lớn, trục nhỉ, tiêu cự và tỉ số \(\dfrac{c}{a}\) của elip (E)
c) Tìm diện tích của hình chữ nhât cơ sở của (E)
a, Phương trình chính tắc của (E) có dạng
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) với 0<b<a
Ta có A(0;2) \(\in\left(E\right)\)<=>b=2
(E) có tiêu điểm F1\(\left(-\sqrt{5};0\right)\) => c=\(\sqrt{5}\)
Ta có \(a^2=b^2+c^2=4+5=9\)=>a=3
==> (E) \(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
b, 2a = 6; 2b = 4; 2c = \(2\sqrt{5}\)=>\(\dfrac{c}{a}=\dfrac{\sqrt{5}}{3}\)
c, S=4ab=24
Đúng 0
Bình luận (0)
Cho tam giác ABC và tam giác có 3 đỉnh là D,E,F. Biết AB= DF và ∠B=∠D
Trong các khẳng định sau,khẳng định nào đúng, khẳng định nào sai ?
a)Nếu ∠A = ∠F thì hai tam giác đó bằng nhau
b)Nếu ∠A = ∠E thì hai tam giác đó bằng nhau
c)Nếu ∠C = ∠E thì hai tam giác đó bằng nhau
a) Đúng. Khi đó, ∆ABC = ∆FDE ( g.c.g)
b) Sai;
c) Đúng.
+)Vì ta có: ∠A + ∠B +∠C = 180º ( tổng ba góc của tam giác).
Và ∠D + ∠E + ∠F = 180º ( tổng ba góc của tam giác)
+) Lại có; ∠B = ∠D; ∠C = ∠E nên ∠A = ∠F
+) Kết hợp giả thiết suy ra: ∆ABC = ∆ FDE ( g.c.g)
Đúng 0
Bình luận (0)
Một (E) có độ dài trục lớn bằng 6, tâm sai bằng \(\dfrac{1}{2}\), khoảng cách từ M thuộc (E) đến tiêu điểm F1 (có hoành độ âm) bằng 7.
a. Tìm khoảng cách từ M đến F2
b. Viết PTCT (E) và tìm M