giải phương trình :
7x3 - 4x2 + 4x + 4 =0
Những câu hỏi liên quan
Giải các phương trình:
b) x 2 - 6 x + 9 - 4 x 2 + 4 x + 1 = 0
Áp dụng công thức nghiệm để giải các phương trình: 4x2 – 4x + 1 = 0
4x2 – 4x + 1 = 0;
a = 4; b = -4; c = 1
Δ = b2 - 4ac = (-4)2 - 4.4.1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
9
−
x
2
x
;
b)
x
−
15
+
1
3
x
;
c)
4
x
2
−
1
+
3
x...
Đọc tiếp
Giải các phương trình sau:
a) 9 − x = 2 x ; b) x − 15 + 1 = 3 x ;
c) 4 x 2 − 1 + 3 x 2 x − 1 = 0 ; d) 5 − 4 x = 4 − 5 x .
Giải phương trình
3
x
+
4
x
-
2
-
1
x
+
2
4...
Đọc tiếp
Giải phương trình 3 x + 4 x - 2 - 1 x + 2 = 4 x 2 - 4 + 3
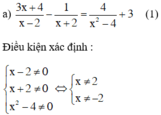
Quy đồng và bỏ mẫu chung ta được:
Phương trình (1) ⇔ (3x + 4)(x + 2) – (x – 2) = 4 + 3(x2 – 4)
⇔ 3x2 + 6x + 4x + 8 – x + 2 = 4 + 3x2 – 12
⇔ 9x = –18
⇔ x = –2 (không thỏa mãn đkxđ)
Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Xác định a, b', c rồi dùng công thức nghiệm thu gọn giải các phương trình:
4x2 + 4x + 1 = 0
Phương trình bậc hai 4x2 + 4x + 1 = 0
Có a = 4; b’ = 2; c = 1; Δ’ = (b’)2 – ac = 22 – 4.1 = 0
Phương trình có nghiệm kép là:
Đúng 0
Bình luận (0)
Xác định a, b, c rồi dùng công thức nghiệm thu gọn giải các phương trình:
a
)
4
x
2
+
4
x
+
1
0
b
)
13852
x
2
−...
Đọc tiếp
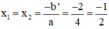
Xác định a, b', c rồi dùng công thức nghiệm thu gọn giải các phương trình:
a ) 4 x 2 + 4 x + 1 = 0 b ) 13852 x 2 − 14 x + 1 = 0 c ) 5 x 2 − 6 x + 1 = 0 d ) − 3 x 2 + 4 6 ⋅ x + 4 = 0
a) Phương trình bậc hai 4 x 2 + 4 x + 1 = 0
Có a = 4; b’ = 2; c = 1; Δ ’ = ( b ’ ) 2 – a c = 2 2 – 4 . 1 = 0
Phương trình có nghiệm kép là:
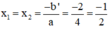
b) Phương trình 13852 x 2 – 14 x + 1 = 0
Có a = 13852; b’ = -7; c = 1;
Δ ’ = ( b ’ ) 2 – a c = ( - 7 ) 2 – 13852 . 1 = - 13803 < 0
Vậy phương trình vô nghiệm.
c) Phương trình bậc hai 5 x 2 – 6 x + 1 = 0
Có: a = 5; b’ = -3; c = 1.; Δ ’ = ( b ’ ) 2 – a c = ( - 3 ) 2 – 5 . 1 = 4 > 0
Phương trình có hai nghiệm phân biệt:
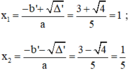
d) Phương trình bậc hai: 
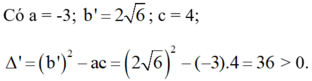
Phương trình có hai nghiệm phân biệt :
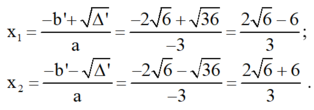
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt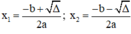 
+ Nếu Δ = 0, phương trình có nghiệm kép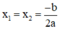 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Áp dụng công thức nghiệm để giải các phương trình:
a
)
5
x
2
−
x
+
2
0
b
)
4
x
2
−
4
x...
Đọc tiếp
Áp dụng công thức nghiệm để giải các phương trình:
a ) 5 x 2 − x + 2 = 0 b ) 4 x 2 − 4 x + 1 = 0 c ) − 3 x 2 + x + 5 = 0
a) 5 x 2 – x + 2 = 0 ;
a = 5; b = -1; c = 2
Δ = b 2 - 4 a c = ( - 1 ) 2 - 4 . 5 . 2
= 1 - 40 = -39 < 0
Vậy phương trình trên vô nghiệm.
b) 4 x 2 – 4 x + 1 = 0 ;
a = 4; b = -4; c = 1
Δ = b 2 - 4 a c = ( - 4 ) 2 - 4 . 4 . 1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
c) - 3 x 2 + x + 5 = 0
a = -3; b = 1; c = 5
Δ = b 2 - 4 a c = 12 - 4 . ( - 3 ) . 5 = 1 + 60 = 61 > 0
⇒ Do Δ >0 nên áp dụng công thức nghiệm, phương trình có 2 nghiệm phân biệt
x 1 = ( 1 - √ 61 ) / 6 ; x 2 = ( 1 + √ 61 ) / 6
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
7
−
x
2
4
−
x
+
5
2
0
;
b)
4
x
2
+
x
−
1...
Đọc tiếp
Giải các phương trình sau:
a) 7 − x 2 4 − x + 5 2 = 0 ;
b) 4 x 2 + x − 1 2 − 2 x + 1 2 = 0 ;
c) x 3 + 1 = x + 1 2 − x ;
d) x 2 − 4 x − 5 = 0 .
Giải phương trình: 4x2 + 4x + 1 = x2.
4x2 + 4x + 1 = x2
⇔ 4x2 + 4x + 1 – x2 = 0
⇔ (4x2 + 4x + 1) – x2 = 0
⇔ (2x + 1)2 – x2 = 0
⇔ (2x + 1 – x)(2x + 1 + x) = 0
(Sử dụng hằng đẳng thức)
⇔ (x + 1)(3x + 1) = 0
⇔ x + 1 = 0 hoặc 3x + 1 = 0
+ x + 1 = 0 ⇔ x = -1.
+ 3x + 1 = 0 ⇔ 3x = -1 ⇔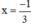 
Vậy phương trình có tập nghiệm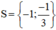 
Đúng 0
Bình luận (0)
2 tháng 4 2022 lúc 8:25
Giải phương trình: 4x2 - 4x + 1 = 9
=>(2x-1)2=9
=>2x-1=3 hoặc 2x-1=-3
=>2x=4 hoặc 2x=-2
=>x=2 hoặc x=-1
Đúng 2
Bình luận (0)
=>(2x-1)2=9
=>2x-1=3 hoặc 2x-1=-3
=>2x=4 hoặc 2x=-2
=>x=2 hoặc x=-1
Đúng 0
Bình luận (0)