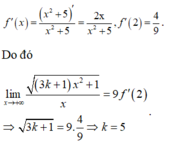Cho f(x)=x2-3x-5, giá trị của \(k\)không âm để f(k)=k là.......

Những câu hỏi liên quan
Cho f(x)= x^2 - 3x - 5 , giá trị k không âm để f(k)=k là ...
ta có
\(f\left(x\right)=x^2-3x-5=x\Leftrightarrow x^2-4x+4=9\)\(\Leftrightarrow\left(x-2\right)^2=3^2\)\(\Leftrightarrow\orbr{\begin{cases}x-2=3\\x-2=-3\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=5\\x=-1\end{cases}}\)
Vậy x=... thì f(k)=k
Đúng 0
Bình luận (0)
cho f(x)=x2-3x-5 giá trị k không âm để f(k)=k là
cho f (x) = x2 - 3x - 5 . tìm k không âm thỏa mãn f (k) = k
f(k)=k
<=> k2-3k-5=k
<=> k2-3k-5-k=0
<=> k2-4k-5=0
<=> k2-4k-4-1=0
<=> (k-2)2=1
<=> k-2=1 hoặc k-2=-1
<=> k=3 hoặc k=1
Đúng 0
Bình luận (0)
Tìm giá trị dương của k để
lim
x
→
+
∞
(
3
k
+
1
)
x
2
+
1
x
9
f
(
2
)
với ...
Đọc tiếp
Tìm giá trị dương của k để lim x → + ∞ ( 3 k + 1 ) x 2 + 1 x = 9 f ' ( 2 ) với f ( x ) = ln ( x 2 + 5 )
A. k = 12
B. k = 2
C. k = 5
D. k = 9
cho f(x)= x2 - 3x -5 , giá trị k không âm để f(k)=k là
Bài 4:: a) Xác định k\(\inℤ\) để giá trị của biểu thức \(k^3+2x^2+15\)chia hết cho giá trị của biểu thức k+3
b) Với giá trị nào của a và b thì đa thức f(x)= \(x^4-3x^3+3x^2+ax+b\)chia hết cho đa thức g(x)=-3x-4
Bài 1: Cho f(x) = 2x2 + x - 7; g(x) = x - 2; h(x) = 10x2 - 7x - 5; k(x) = 2x - 3
Tìm x thuộc Z để:
a) Giá trị của f(x) \(⋮\)giá trị của g(x)
b) Giá trị của h(x) chia hết cho giá trị của k(x)
1/ B chia đa thức f(x) cho g(x) như bình thường, dư 3
Để chia hết, số dư phải bằng 0
hay x- 2 thuộc ước của 3 bằng \(\pm1,\pm3\)
Ta có bảng gt:
.....
Vậy..........
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thức sau
E=(2x – 5)10 – 12 F=(x+5)8+|x+5|+ 22
Tìm giá trị lớn nhất của các biểu thức sau
G=17-|3x-2| K= 17-|3x-2|- (2-3x)2020
\(E=\left(2x-5\right)^{10}-12\ge-12\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{5}{2}\)
Vậy \(E_{min}=-12\Leftrightarrow x=\dfrac{5}{2}\)
\(F=\left(x+5\right)^8+\left|x+5\right|+22\ge22\)
Dấu "=" xảy ra \(\Leftrightarrow x=-5\)
Vậy \(F_{min}=22\Leftrightarrow x=-5\)
\(G=17-\left|3x-2\right|\)
Dấu "=" xảy ra \(x=\dfrac{2}{3}\)
Vậy \(G_{max}=17\Leftrightarrow x=\dfrac{2}{3}\)
\(K=17-\left|3x-2\right|-\left(2-3x\right)^{2020}\le17\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{2}{3}\)
Vậy \(K_{max}=17\Leftrightarrow x=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
cho đa thức f(x)=x^4+(2-k)x^2+5-k (với k là hằng số tự nhiên có trước ).biết đa thức f(x)có đúng 3 nghiệm phân biệt.hãy tính giá trị 24-4k