`bạn tự kẻ hình nhé
ta đễ dàng cm dk DM=CM
Từ đó ta có SAMDAMD=1/2 SDACDAC=1/3 SABCABC
SBDMBDM = 1/2SBDCBDC= 1/6 SABCABC
Suy ra SABMABM=(1/3+1/6)SABCABC= 1/2SABCABC= 15m^2

cho hỏi là làm sao dm=cm

Đặt S_AKE = x,  S_AKD = y

Ta có S_BKE = 2x, S_CKD = y.

Ta có:

S A B D = 15 c m 2 ⇒ 3 x + y = 15     ( 1 ) S A C E = 10 c m 2 ⇒ x + 2 y = 10    ( 2 )  

Þ x = 4cm², y = 3cm²

Þ S_ADKE = 7cm²

Câu 9 ) 

Theo bài ra , ta có : 

\(m+\frac{1}{n+\frac{1}{p}}=\frac{17}{3}\)

\(\Leftrightarrow m+\frac{1}{n+\frac{1}{p}}=5\frac{2}{3}\)

\(\Leftrightarrow m=5\)

\(\Leftrightarrow\frac{1}{n+\frac{1}{p}}=\frac{2}{3}\)

\(\Leftrightarrow n+\frac{1}{p}=\frac{3}{2}\)

\(\Leftrightarrow n+\frac{1}{2}=\frac{3}{2}\)( p không thể là 1 vì \(\frac{1}{p}=1\)) 

\(\Leftrightarrow n=\frac{3}{2}=\frac{1}{2}=1\)

Vậy n = 1 

Chúc bạn học tốt =)) 

VÒNG 13

C10            12cm²

khó vậy vì em mới học lớp 6

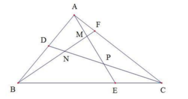
CPE = 1/3 CPB = 1/3 CPA=1/4 CAE=1/8 ABC

BND=1/2 BNA=1/6 BNC=1/7 BCD=1/14ABC

AMF=1/4 AMC=1/8 ABM= 1/9 ABF=1/36 ABC

AMND=ABF – BND – AMF

=1/4 ABC = 1/14 ABC = 1/36 ABC= 7/42 ABC

BEPD= BCD = CPE

= ½ ABC – 1/8 ABC = 3/8 ABC

MNP = ABC – AEC – BEPD – AMND

= ABC – 1/3 ABC – 3/8 ABC – 7/42 ABC

= 1/8 ABC

từ I kẻ IM vuông góc AC , từ B kẻ BN vuông góc AC  => IM // BN

áp dụng định lý Menelous vào tam giác BCD có 3 điểm A ,I , E thẳng hàng và cắt 3 cạnh tam giác :

\(\dfrac{EC}{EB}\cdot\dfrac{IB}{ID}\cdot\dfrac{AD}{AC}=1\)

=> 2 . \(\dfrac{IB}{ID}\) .  3/4  = 1

=> \(\dfrac{IB}{ID}=\dfrac{4}{3}\)

\(\Rightarrow\dfrac{DI}{DB}=\dfrac{3}{7}\)

Do IM // BN => \(\dfrac{DI}{DB}=\dfrac{IM}{BN}=\dfrac{3}{7}\) 

S abc = \(\dfrac{1}{2}BN\cdot AC\)     

S iad = \(\dfrac{1}{2}IM\cdot AD\)         \(\Rightarrow\dfrac{Siad}{Sabc}=\dfrac{IM}{BN}\cdot\dfrac{AD}{AC}=\dfrac{3}{7}\cdot\dfrac{3}{4}=\dfrac{9}{28}\)

mà S iad = 18  => S abc = 28*18 : 9 = 56