cho tam giác ABC có \(\widebat{A}\)=30 độ, dựng bên ngoài tam giác đó tam giác BCD đều.Nối A với D. Chứng minh AB2+AC2=AD2

Những câu hỏi liên quan
Cho tam giác ABC có ba góc nhọn và AH là đường caoa, Chứng minh:
A
B
2
+
C
H
2
A
C
2
+
B
H
2
b, Vẽ trung tuyến AM của tam giác ABC, chứng minh:1.
A
B...
Đọc tiếp
Cho tam giác ABC có ba góc nhọn và AH là đường cao
a, Chứng minh: A B 2 + C H 2 = A C 2 + B H 2
b, Vẽ trung tuyến AM của tam giác ABC, chứng minh:
1. A B 2 + A C 2 = B C 2 2 + 2 A M 2
2. A C 2 - A B 2 = 2 B C . H M (với AC > AB)
a, Sử dụng định lí Pytago cho các tam giác vuông HAB và HAC để có đpcm
b, 1. Chứng minh tương tự câu a)
2. Sử dụng định lí Pytago cho tam giác vuông AHM
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn,góc A bằng 30 độ.Trên nưả mp bờ BC ko chứa A,vẽ tam giác BCD đều.CMR:AD2=AB2+AC2
cho tam giac abc có abc =40 độ, acb =30 độ. bên ngoài dựng tam giác ACD có góc acd=cad=50 độ. chứng minh tam giác bad cân
cho tam giac abc có abc =40 độ, acb =30 độ. bên ngoài dựng tam giác ACD có góc acd=cad=50 độ. chứng minh tam giác bad cân
cho tam giac abc có abc =40 độ, acb =30 độ. bên ngoài dựng tam giác ACD có góc acd=cad=50 độ. chứng minh tam giác bad cân
cho tam giác ABC. Góc A = 30 độ . Dựng ở ngoài tam giác ABC tam giác đều BCD. CMR: AD^2=AB^2+AC^2
Về phía ngoài \(\Delta\)ABC dựng tam giác đều ACE.
Ta có: ^ACB + 600 = ^ACB + ^BCD = ^ACB + ^ACE => ^ACD = ^ECB.
Xét \(\Delta\)DAC và \(\Delta\)BEC: DC = BC, ^ACD = ^ECB, AC = EC
=> \(\Delta\)DAC = \(\Delta\)BEC (c.g.c) => AD = EB (2 cạnh tương ứng).
Lại có: ^BAE = ^BAC + ^CAE = 900. Áp dụng ĐL Pytagore cho \(\Delta\)ABE vuông tại A:
EB2 = AB2 + AE2 . Thay AD = EB (cmt) và AE = AC (Vì \(\Delta\)ACE đều) ta được: AD2 = AB2 + AC2 (đpcm).
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác abc cân tại a kẻ ah vuông góc với bc
chứng minh rằng tam giác ahb = tam giác ahc
chứng minh hc=hb
kẻ hd vuông góc ab;he vuông góc ac chứng minh tam giác hde cân;
ab2-ad2=dh2-bh2
a) Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Dựng bên ngoài tam giác ABC các tam giác đều ABE và ACF. Dựng hình bình hành AEDF. Chứng mình BCD là tam giác đều
giúp mình với, mai nộp rồi, thanks!
Xét tam giác ABD và tam giác FBC có:
AB=FB ( cạnh tam giác đều FAB)
DB=BC ( cạnh tam giác đều DBC)
góc ABD = góc FBC ( cùng bằng góc ABC + 60 độ)
Suy ra tam giác ABD = tam giác FBC (c.g.c)
=> FC=AD
Đúng 0
Bình luận (2)
Cho tam giác ABC có ∠A = 60 0 Chứng minh rằng:
B C 2 = A B 2 + A C 2 - AB.AC
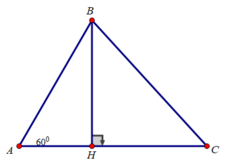
Kẻ đường cao BH
Xét tam giác ABH vuông tại H có ∠(BAC) = 60 0
BH = AB.sin A = AB.sin 60 0 = (AB 3 )/2
AH = AB.cos A = AB.cos 60 0 = AB/2
Xét tam giác BHC vuông tại H có:
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2
= B H 2 + A C 2 - 2 A C . A H + A H 2
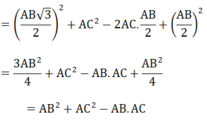
Vậy được điều phải chứng minh.
Đúng 0
Bình luận (0)














