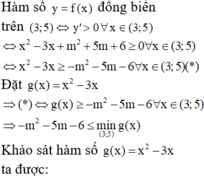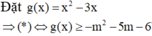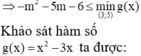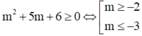Tìm m để hàm số y=(3m2 +5m+2 )x-5m+1 đồng biến trên R

Những câu hỏi liên quan
Tìm m để hàm số y=(3m2 +5m+2 )x-5m+1 đồng biến trên R
Hàm số có dạng y = ax + b đồng biến nếu a > 0; nghịch biến nếu a < 0
(Đồng biến nghĩa là: Nếu x1 < x2 thì y1 < y2) (Em xem lại trong SGK 9 có nhắc)
Để hàm số đồng biến trên R <=> 3m2 + 5m + 2 > 0
<=> 3m2 + 3m + 2m + 2 > 0
<=> 3m(m +1) + 2.(m+1) > 0
<=> (3m +2).(m +1) > 0
=> 3m + 2 và m + 1 cùng dấu
TH1: 3m +2 > 0 và m + 1 > 0
=> m > -2/3 và m > -1 => m > -2/3
TH2: 3m + 2 < 0 và m + 1 < 0
=> m < -2/3 và m < -1 => m < -1
Vậy với m > -2/3 hoặc m < -1 thì hàm số đồng biến
Đúng 1
Bình luận (0)
tìm m để hàm số đồng biến trên R
y=\(\frac{1}{3}\)x^3+(m+1)x^2+(5m-1)x-m
Cho hàm số
y
m
+
5
m
-
5
.
x
+
2010
Tìm các giá trị của m để hàm số đã cho là hàm số bậc nhất đồng biến trê...
Đọc tiếp
Cho hàm số y = m + 5 m - 5 . x + 2010
Tìm các giá trị của m để hàm số đã cho là hàm số bậc nhất đồng biến trên R.
Với điều kiện m ≥ 0 và m ≠ 5 thì m + 5 > 0. Do đó, điều kiện để hàm số đã cho là hàm số bậc nhất đồng biến trên R là: m - 5 > 0, suy ra m > 5 ⇔ m > 5.
Đúng 0
Bình luận (0)
Cho hàm số
y
(
m
2
–
1
)
x
+
5
m
. Tìm m để hàm số là hàm số đồng biến trên . A. m −1 B. m 1 C. m −1 D.
m
1
;
m
−
1
Đọc tiếp
Cho hàm số y = ( m 2 – 1 ) x + 5 m . Tìm m để hàm số là hàm số đồng biến trên .
A. m < −1
B. m > 1
C. m > −1
D. m > 1 ; m < − 1
Hàm số y = ( m 2 – 1 ) x + 5 m là hàm số đồng biến khi m 2 – 1 > 0
⇔ ( m – 1 ) ( m + 1 ) > 0
TH1: m − 1 > 0 m + 1 > 0 ⇔ m > 1 m > − 1 ⇔ m > 1
TH2: m − 1 < 0 m + 1 < 0 ⇔ m < 1 m < − 1 ⇔ m < − 1
Vậy m > 1 m < − 1
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Tìm tập hợp các giá trị của tham số thực m để hàm số ymsinx+7x-5m+3 đồng biến trên R A.. B.. C.. D..
Đọc tiếp
Tìm tập hợp các giá trị của tham số thực m để hàm số y=msinx+7x-5m+3 đồng biến trên R
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Chọn A
Ta có![]() .
.
![]() .
.
Hàm số ![]() đồng biến trên
đồng biến trên ![]() khi
khi ![]()
![]() .
.
Ta có ![]()
![]() .
.
+TH1 ![]()
![]()
![]()
![]() .
.
+TH2 ![]()
![]()
![]()
![]() .
.
Vậy ![]() .
.
Đúng 0
Bình luận (0)
Cho hàm số: y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
a) Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
b) Với giá trị nào của m thì hàm số đạt cực đại tại x = 1 ?
a) y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+) m2 + 5m = 0 ⇔ 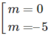
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
Δ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
b) Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
y′(1) = –3
m
2
– 3m + 6 = 0 ⇔ 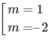
Mặt khác, y” = –6( m 2 + 5m)x + 12m
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm
y
x
2
-
3
x
+
m
2
+
5
m
+
6
. Tìm tất cả các giá trị của m để hàm số đồng biến trên (3;5) A. B. C. D. Với mọi
Đọc tiếp
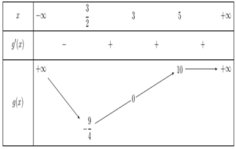
Cho hàm số y=f(x) có đạo hàm y ' = x 2 - 3 x + m 2 + 5 m + 6 . Tìm tất cả các giá trị của m để hàm số đồng biến trên (3;5)
A. ![]()
B.![]()
C. ![]()
D. Với mọi ![]()
Cho hàm số y f(x) có đạo hàm
y
x
2
-
3
x
+
m
2
+
5
m
+
6
. Tìm tất cả các giá trị của m để hàm số đồng biến trên (3;5)
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm y ' = x 2 - 3 x + m 2 + 5 m + 6 . Tìm tất cả các giá trị của m để hàm số đồng biến trên (3;5)
![]()
![]()
![]()
![]()
Cho hàm số: y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5. Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+)
m
2
+ 5m = 0 ⇔ 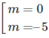
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
∆ ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
Đúng 0
Bình luận (0)