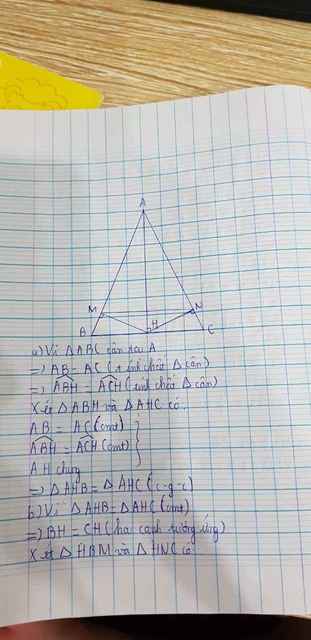a: Sửa đề: Trên tia đối của tia AC lấy N sao cho AN=AC

Xét ΔABC và ΔAMN có

AB=AM

\(\widehat{BAC}=\widehat{MAN}\)(hai góc đối đỉnh)

AC=AN

Do đó: ΔABC=ΔAMN

b; Ta có: ΔABC=ΔAMN

=>BC=MN

Ta có: ΔABC=ΔAMN

=>\(\widehat{ABC}=\widehat{AMN}\)

mà hai góc này là hai góc ở vị trí so le trong

nên BC//MN

a) Xét tam giác AHB vuông tại H và tam giác AHC vuông tại H:

AB = AC (Tam giác ABC cân tại A).

\(\widehat{B}=\widehat{C}\) (Tam giác ABC cân tại A).

\(\Rightarrow\Delta AHB=\Delta AHC\left(ch-gn\right).\)

b) Xét tam giác ABC cân tại A:

AH là đường cao (AH ⊥ BC).

\(\Rightarrow\) AH là đường trung tuyến (T/c tam giác cân).

\(\Rightarrow\) H là trung điểm BC.

Xét tam giác MBH vuông tại M và tam giác NCH vuông tại N:

BH = CH (H là trung điểm BC).

\(\widehat{B}=\widehat{C}\) (Tam giác ABC cân tại A).

\(\Rightarrow\Delta MBH=\Delta NCH\left(ch-gn\right).\\ \Rightarrow BM=CN.\)

Ta có: \(AM=AB-BM;AN=AC-CN.\)

Mà \(\left\{{}\begin{matrix}AB=AC\\BM=CN\end{matrix}\right.\) (cmt).

\(\Rightarrow AM=AN.\Rightarrow\Delta AMN\) cân tại A.

c) Xét tam giác AMN cân tại A:

\(\widehat{AMN}=\dfrac{180^o-\widehat{A}}{2}.\)

Xét tam giác ABC cân tại A:

\(\widehat{ABC}=\dfrac{180^o-\widehat{A}}{2}.\)

\(\Rightarrow\widehat{AMN}=\widehat{ABC}.\\ \Rightarrow MN//BC\left(dhnb\right).\)

a) xét ΔAHB và ΔAHC có:

góc H1=góc H2=90độ

AH chung

góc B=góc C (ΔABC cân tại A)

=> ΔABH=ΔAHC(CH−GN)

=>góc A1=góc A2(2 góc tương ứng)

b) xét ΔAHN và ΔAHM có:

góc M=góc N=90độ

AH chung

góc A1=góc A2(cmt)

=> ΔAHN=ΔAHM(CH−CN)

=> HN = HM (2 cạnh tương ứng)

=> AN = AM (2 cạnh tương ứng)

ΔAMN có: AN = AM (cmt)

=> ΔAMN cân tại A

c) đặt điểm giao nhau giữa AH và MN là K

xét ΔAKM và ΔAKN có:

AK chung

góc A1=góc A2(cmt)

AM = AN (ΔAMN cân tại A)

=> ΔAKM=ΔAKN(c.g.c)

=> góc K1=góc K2

mà 2 góc trên ở vị trí kề bù

=> góc K1=góc K2=90độ

=> MN ⊥AH

mà BC⊥AH

=> MN // BC (tính chất)

b) Vì hai tam giác ở trên bằng nhau nên CD=AM=MB

Vì CD//AM hay CD//MB=> góc DCM=BMC(slt)

Xét tamg iasc MCD và CMB có

BM=CD(cmt)

góc DCM=BMC(cmt)

MC cạnh chung

vậy hai tam giác băng nhau theo trường hợp(c.g.c)

c) Vì tam giác MCD=CMB nên  góc DMC=BCM(góc tương ứng)

mà chúng ở vị trí so le trong nên MD//BC hay MN//BC.

và MD=BC, mà MN=1/2MD=> MN=BC/2

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có

AB=AC

AH chung

Do đó: ΔABH=ΔACH

b: BH=6/2=3(cm)

Xét ΔABH vuông tại H có \(AB^2=AH^2+HB^2\)

hay \(AH=\sqrt{8^2-3^2}=\sqrt{55}\left(cm\right)\)

c: Xét ΔAHM vuông tại M và ΔAHN vuông tại N có

AH chung

\(\widehat{MAH}=\widehat{NAH}\)

Do đó: ΔAHM=ΔAHN

Suy ra: AM=AN

Xét ΔABC có AM/AB=AN/AC

nên MN//BC

Bài 1:

a: Xét ΔBNM có AD//NM

nên MN/AD=BM/BD

=>MN*BD=AD*BM

b: ME/AD=CM/CD=CM/BD

MN/AD+ME/AD=BM/BD+CM/BD=BC/BD=2

c:

Xét ΔBÂC có BE là phân giác

nen CE/CA=BC/BA

=>MC/MD=CE/CA=BC/BA

Ta có : \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\left(gt\right)\Rightarrow\)MN//BC 

a, Ta có : BC² = 10² = 100

AB² + AC² = 6² + 8² = 36 + 64 = 100

=> AB² + AC² = BC²

=> Tam giác ABC vuông tại A ( Định lý Py - ta - go đảo )

Study well ! >_<

a)Xét\(\Delta ABC\)có:\(BC^2=10^2=100\)

\(AB^2+AC^2=6^2+8^2=36+64=100\)

Ta thấy:\(BC^2=AB^2+AC^2\left(=100\right)\)

\(\Rightarrow\Delta ABC\)cân tại A(Định lí Py-ta-go)

b)Xét\(\Delta MAB\)và\(\Delta MNB\)có:

MB là cạnh chung

\(\widehat{MAB}=\widehat{MNB}\left(=90^o\right)\)

\(\widehat{MBA}=\widehat{MBN}\)(BM là tia p/g của \(\widehat{ABN}\))

Do đó:\(\Delta MAB=\Delta MNB\)(cành huyền-góc  nhọn)

\(\Rightarrow MA=MN\)(2 cạnh t/ứ)

c)Xét\(\Delta MAP\)và\(\Delta MNC\)có:

\(MA=MN\)(cmt)

\(\widehat{AMP}=\widehat{NMC}\)(2 góc đối đỉnh)

\(\widehat{MAP}=\widehat{MNC}\left(=90^o\right)\)

Do đó:\(\Delta MAP=\Delta MNC\)(cạnh gv-góc nhọn)

\(\Rightarrow MP=MC\)(2 cạnh t/ứ)

Ta có:MN<MC(ĐL mối QH giữa đường vg và đg xiên)

mà MC=MP(cmt)

\(\Rightarrow MN< MP\)hay MP>MN

Lúc nãy mik đánh nhầm căn cứ câu a bn sửa lại thành "Định lí Py-ta-go đảo" nhé!!!!