Cho tam giác nhọn ABC có góc A =60 độ và 2 đường phân giác BD và CE cắt nhau tại I. Chứng minh rằng tam giác IDE cân.

Những câu hỏi liên quan
Cho tam giác nhọn ABC có góc A =60 độ và 2 đường phân giác BD và CE cắt nhau tại I. Chứng minh rằng tam giác IDE cân.
Cho tam giác ABC có góc B=600.Hai đường phân giác AD và CE của góc A và C cắt nhau tại I (D thuộc BC và E thuộc AB).Chứng minh tam giác IDE cân
Trên AC lấy F sao cho AE=AF
Xét ΔAEI và ΔAFI co
AE=AF
góc EAI=góc FAI
AI chung
Do đó: ΔAEI=ΔAFI
=>EI=FI
góc IAC=180 độ-góc IAC-góc ICA
=180 độ-1/2*120
=120 độ
=>góc AIE=góc DIC=60 độ
góc AIF=góc AIE=60 độ
Xet ΔDIC và ΔFIC có
góc DCI=góc FCI
CI chung
góc DIC=góc FIC
Do đó: ΔDIC=ΔFIC
=>ID=IF
=>ID=IE
=>ΔIDE cân tại I
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB<AC, góc B=60 độ. Hai tia phân giác AD và CE của tam giác ABC cắt nhau ở I . Chứng minh tam giác IDE cân
tha khảo
vì p>3 nên p có dạng p=3k+1 hoặc p=3k+2
với p=3k+1 thì p^2-1=(p+1)(p-1)=(3k+2)3k chia hết cho 3
với p=3k+2 thì p^2-1=(p+1)(p-1)=(3k+3)(3k+1) chia hết cho 3
vậy với mọi số nguyên tố p>3 thì p^2-1 chia hết cho 3 (1)
mặt khác cũng vì p>3 nên p là số lẻ =>p+1,p-1 là 2 số chẵn liên tiếp
=>trong hai sô p+1,p-1 tồn tại một số là bội của 4
=>p^2-1 chia hết cho 8 (2)
từ (1) và (2) => p^2-1 chia hết cho 24 với mọi số nguyên tố p>3
Đúng 0
Bình luận (0)
Cho tam giác abc có góc B=60 độ. Phân giác AD và CE của tam giác ABC cắt nhau ở I, từ trung điểm M của BC kẻ đường vuông góc vs phân giác AI tại H, cắt AB ở P cắt AC ở K. Chứng minh:
a) Tính goác AIC
b) Tính độ dài cạnh AK biết PK=6cm, AH=4cm
c) Chứng minh rằng tam giác IDE cân
Cho tam giác ABC (AB <AC có góc B= 60 độ ). Hai phân giác AD và CE của tam giác ABC cắt nhau ở I, từ trung điểm M của BC kẻ đường vuông góc với đường phân giác AI tại H, cắt AB ở P, cắt AC ở K. a) Tính góc AIC b) Tính độ dài cạnh AK biết PK = 6cm, AH = 4 cm. c) Chứng minh tam giác IDE cân.
nhầm lớp thì phải
a)cho tam giác ABC có các đường cao BD và CE bằng nhau . Chứng minh rằng tam giác đó là một tam giác cân
b)Cho tam giác ABC cân tại A,đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC
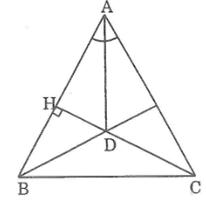
Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.
Suy ra: AD ⊥ BC
Ta có: CH ⊥ AB (gt)
Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC
Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.
Vậy BD ⊥ AC.
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có góc A=60 độ và hai đường phân giác BD và CE cắt nhau ở I
1) Tính số đo góc BIC
2) IF đường phân giác của tam giác IBC .Chứng minh tam giác BIE=tam giác BIF
Câu 4: cho tam giác ABC cân tại A.Hai đường phân giác BD và CE cắt nhau tại I . Chứng minh a, BD=CE b,ED//BC c,BE=ED=DC d,Khi góc BAC=60,BD=6cm.Hãy tính chu vi tam giác ABC
Cho tam giác ABC nhọn, AB>AC, phân giác BD và CE cắt nhau tại I.a)tính các góc của tam giác DIE nếu góc A= 60 độ,b) gọi giao điểm cña BD và CE với đường cao AH của tam giác ABC lần lượt là M và N .chứng minh: BM > MN + NC.
nói bậy bạn ơi chưa khi nào đọc nội quy à



















