DEBF có EB // DF ; EB = \(\frac{1}{2}\).AB = \(\frac{1}{2}\).DC = FC 

=> DEBF là hình bình hành

Vì AB = CD (định lý)

mà EA = EB = FD = FC 

Ta có :

AB // CD (gt) => EB // DF 

=> EBFD là hình bình hành 

Bài 2:

AK=AB/2

CI=CD/2

mà AB=CD

nên AK=CI

Xét tứ giác AKCI có

AK//CI

AK=CI

Do đó: AKCI là hình bình hành

=>AC cắt KI tại trung điểm của mỗi đường(1)

ABCD là hình bình hành

=>AC cắt BD tại trung điểm của mỗi đường(2)

Từ (1) và (2) suy ra AC,KI,BD đồng quy

Bài 1:

a: \(\widehat{ADE}=\widehat{EDF}=\dfrac{1}{2}\cdot\widehat{ADC}\)

\(\widehat{ABF}=\widehat{CBF}=\dfrac{1}{2}\cdot\widehat{ABC}\)

mà \(\widehat{ADC}=\widehat{ABC}\)

nên \(\widehat{ADE}=\widehat{EDF}=\widehat{ABF}=\widehat{CBF}\)

Xét ΔEAD và ΔFCB có

\(\widehat{A}=\widehat{C}\)

AD=CB

\(\widehat{EDA}=\widehat{FBC}\)

Do đó: ΔEAD=ΔFCB

=>\(\widehat{AED}=\widehat{CFB}\)

=>\(\widehat{EDF}=\widehat{CFB}\)

mà hai góc này đồng vị

nên DE//BF

b: Xét tứ giác DEBF có

DE//BF

BE//DF

Do đó: DEBF là hình bình hành

a Xét tứ giác DEBF có

BE//DF

BE=FD

Do đó; DEBF là hình bình hành

=>DB cắt EF tại trung điểm của mỗi đường(1)

b: Vì ABCD là hình bình hành

nên AC cắt BD tại trung điểm của mõi đường(2)

Từ (1), (2) suy ra AC,BD,EF đồng quy

=>E,O,F thẳng hàng

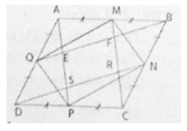
a) Ta có AB // CD (gt)

Suy ra AM // CP    (1)

Lại có AM = AB/2; CP = CD/2    (2)

Từ (1) và (2) suy ra AMCP là hình bình hành

Suy ra AP // CM hay ES // FR.

Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.

Vậy tứ giác EFRS là hình bình hành

b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)

Từ đó suy ra RF = ES = AE = 2x

Suy ra: ES = 2AP/5 => SEFRS = 2SAMCP/5

Vì SAMCP = SABCD/2 nên SEFRS = SABCD/2

a) Gợi ý: Chứng minh QCGA và CRDP là hình bình hành;

b) Chứng minh DQCM = DGAB để suy ra QRGP là hình bình hành;

c) Có

S R C B = 1 3 . S B C D = 1 6 . S A B C D  

Và

S C G D = 1 3 . S A C D = 1 6 . S A B C D  Þ ĐPCM.