chứng minh định lí Xê-va và định lí Meelenauyet bằng đinh lí talet với

Những câu hỏi liên quan
Chứng minh định lí Xê va và định lí Meelenauyt bằng định lí ta let
Chứng minh định lí Talet thuận.
Định lí talet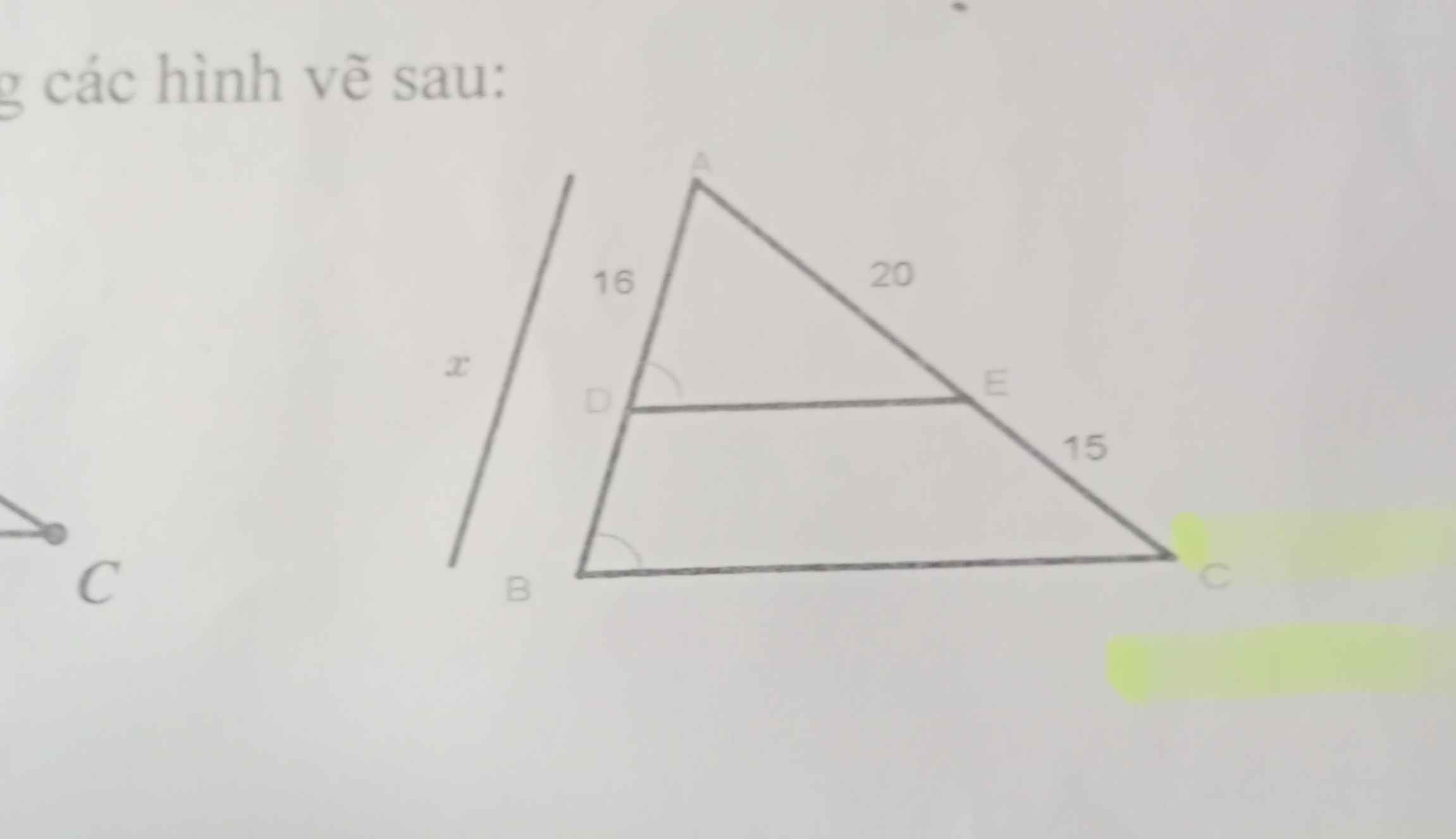
Áp dụng đl ta-lét vào tam giác ABC có DE//BC có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
hay \(\dfrac{16}{DB}=\dfrac{20}{15}\Rightarrow DB=16:\dfrac{20}{15}=12\)
\(\Rightarrow x=AD+DB=16+12=28\)
Đúng 0
Bình luận (0)
Chứng minh định lí: trong một tam giác cân , hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.?
Và
Hãy chứng minh định lí đảo của định lí trên: nếu hai tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân
Cho định lí:
“ Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”.
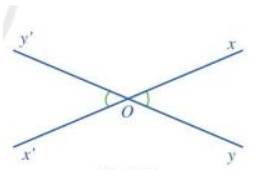
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết và kết luận của định lí trên.
c) Chứng tỏ định lí trên là đúng.
a)
b)
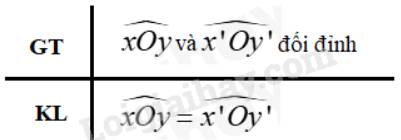
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)
Đúng 0
Bình luận (0)
Chứng minh đinh lí đảo của định lí trên :Nếu tam giavs có 2 đương trung tuyến = nhau thì tam giác đó cân
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Talet đảo.
Định lí Talet đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
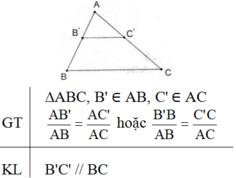
Đúng 0
Bình luận (0)
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Talet trong tam giác.
Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
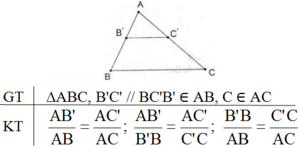
Đúng 0
Bình luận (0)
Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Talet.
Hệ quả của định lí Talet:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.
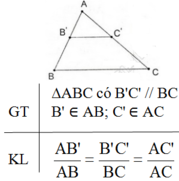
Đúng 0
Bình luận (0)












