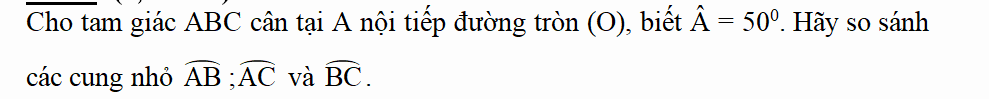Cứu toy chời ơi=((

Những câu hỏi liên quan
chán quá đi chời ơi
her/strong/are/arm
SOS chớt tui chời ơi!
Xem thêm câu trả lời
Chời ơi, tui cần gấp bài vẽ về đề tài trò chơi dân gian, đơn giản, dễ vẽ(đừng phức tạp quá, ko biết vẽ :v)
viết số tự nhiên lớn nhất có các chữ số khác nhau chia hết cho 5 mà tổng các chữ số = 25
ai giúp tui dải nữa với chời ơi khó như đồ quỷ
Xem thêm câu trả lời


giúp tui chời
viết đoạn văn khoảng 20 dòng ghi lại cảm súc của em về đoạn thơ sau: thương cha nhiều lắm cha ơi cày sâu cuốc bẩm, một đời của tra ban mai trưa mở chiều tà sương rơi uồng tráng bên đời vai tra mái ấm bầu chời tình thương dìu con từng bước từng, đường lo toan vất vả đêm trường lằm canh ( phương tra-lê thế thành)
trời ơi cứu tui cứu tui
Ta có \(\dfrac{a^3}{a^2+b^2}=a-\dfrac{ab^2}{a^2+b^2}\ge a-\dfrac{ab^2}{2ab}=a-\dfrac{b}{2}=\dfrac{2a-b}{2}\)(áp dụng cosi cho \(a^2+b^2\ge2ab\))
\(\dfrac{b^3}{b^2+1}=b-\dfrac{b}{b^2+1}\ge b-\dfrac{b}{2b}=b-\dfrac{1}{2}=\dfrac{2b-1}{2}\)(áp dụng cosi cho\(b^2+1\ge2b\))
\(\dfrac{1}{a^2+1}=1-\dfrac{a^2}{a^2+1}\ge1-\dfrac{a^2}{2a}=1-\dfrac{a}{2}=\dfrac{2-a}{2}\)( áp dụng cosi cho \(a^2+1\ge2a\))
Cộng vế theo vế
\(\dfrac{a^3}{a^2+b^2}+\dfrac{b^3}{b^2+1}+\dfrac{1}{a^2+1}\ge\dfrac{2a-b+2b-1+2-a}{2}\)\(\ge\dfrac{a+b+1}{2}\left(đpcm\right)\)
Dấu "=" xảy ra <=> a=b=1
Đúng 2
Bình luận (0)
CÓ AI KB VS TUJ K V CHỜI???
 cấp cứu mn ơi
cấp cứu mn ơi