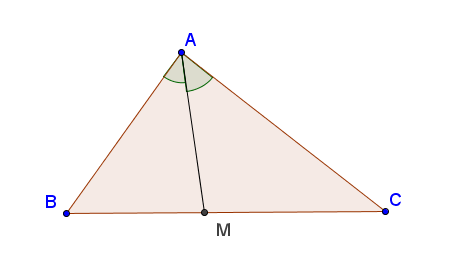
chứng minh rằng trong tam giác đều trọng tâm và giao điểm của 2 đường phân giác trong tam giác trùng nhau

Những câu hỏi liên quan
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:
a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;
b) Nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.
a)
Ta có:
G là trọng tâm của tam giác ABC (giao điểm của ba đường trung tuyến);
H là trực tâm của tam giác ABC (giao điểm của ba đường cao);
I là giao điểm của ba đường phân giác của tam giác ABC;
O là giao điểm của ba đường trung trực của tam giác ABC (Đường trung trực đi qua trung điểm của cạnh và vuông góc với cạnh tại trung điểm đó).
Mà tam giác ABC đều nên trong tam giác ABC đường trung tuyến đồng thời là đường cao và là đường phân giác.
Vậy bốn điểm G, H, I, O trùng nhau hay nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau.
b)
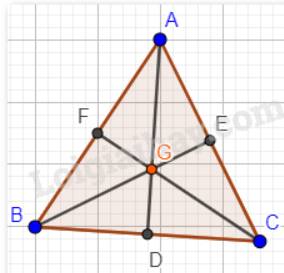
Giả sử trong tam giác ABC có hai điểm trùng nhau là H (trực tâm của tam giác) và I (giao của ba đường phân giác).
Hay AD, BE, CF vừa là đường cao, vừa là đường phân giác của tam giác ABC.
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\) ( vì AD là tia phân giác của góc BAC)
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\) (vì \(AD \bot BC\));
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta AEB = \Delta CEB\)(c.g.c). Suy ra: AB = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều hay nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi G là trọng tâm tam giác. H là trực tâm tam giác. I là giao điểm 3 đường phân giác. O là điểm cách đều 3 đỉnh tam giác.
Chứng minh rằng: tam giác ABC là tam giác đều khi và chỉ khi các điểm G,H,I,O trùng nhau và ngược lại.
Thiên Ngoại Phi Tiên sai rồi cậu lấy trêm mạn mà đúng gì nẫu nói G là trực tâm H là đường cao , o cách đều ba đỉnh mà sao không có ba diểm đó
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng trong 1 tam giác, trọng tâm, trực tâm, giao điểm 3 đường trung trực và giao điểm 3 đường phân giác thẳng hàng.
Chứng minh rằng trong tam giác đều, điểm cách đều 3 cạnh của tam giác là trọng tâm của tam giác đó.

Vì \(\Delta ABC\) đều nên AB = AC = BC (tính chất tam giác đều)
Vì I là điểm cách đều 3 cạnh của tam giác nên là giao điểm của 3 đường phân giác của tam giác ABC
Áp dụng ví dụ 2, ta được, AI là đường trung tuyến của \(\Delta ABC\)
Tương tự, ta cũng được BI, CI là đường trung tuyến của \(\Delta ABC\)
Vậy I là giao điểm của ba đường đường trung tuyến của \(\Delta ABC\) nên I là trọng tâm của \(\Delta ABC\).
Chú ý:
Với tam giác đều, giao điểm của 3 đường trung tuyến cũng là giao điểm của 3 đường phân giác.
Đúng 0
Bình luận (0)
cho tam giác ABC với AB = 5cm, AC = 6cm, BC = 7cm. Gọi G là trọng tâm của tam giác ABC, O là giao điểm của 2 tia phân giác trong của tam giác ABC. Chứng minh rằng GO // AC
Bạn xem lời giải ở đường link sau nhé:
Câu hỏi của Thanh Thanh - Toán lớp 8 - Học toán với OnlineMath
Cho tam giác ABC. Dựng ra ngoài tam giác này các tam giác đều ABD, BCE, CAF. Chứng minh rằng trọng tâm của tam giác DEF trùng với trọng tâm của tam giác ABC.
Vẽ hình bình hành DAFH.
Gọi N là giao điểm của hai đường chéo DF và AH, M là giao điểm của EH và BC
Ta có NA = NH, ND = NF
Ta đặt ^ADH = ^AFH = \(\alpha\)thì ^BDH = ^HFC = \(\alpha\)+ 600
^DAF = 1800 -\(\alpha\)
^BAC = 3600 - ^BAD - ^CAF - ^DAF = 3600 - 600 - 600 - (1800 - \(\alpha\)) = \(\alpha\)+ 600
\(\Delta\)BDH và \(\Delta\)HFC có: BD = HF (= AD); ^BDH = ^HFC (cmt); DH = FC (= AF)
Do đó \(\Delta\)BDH = \(\Delta\)HFC (c.g.c) => HB = HC (1)
Chứng minh tương tự, ta được \(\Delta\)BAC = \(\Delta\)HFC (c.g.c) => BC = HC (2)
Từ (1) và (2) suy ra HB = HC = BC
Tứ giác BHCE có các cặp cạnh đối bằng nhau (cùng bằng BC) nên là hình bình hành => MB = MC và MH = ME
Xét ∆AEH có AM và AN là hai đường trung tuyến nên giao điểm G của chúng là trọng tâm => EG = 2/3EN và AG = 2/3AM.Xét ∆ABC có AM là đường trung tuyến mà AG = 2/3AM nên G là trọng tâm của ∆ABCXét ∆EDF có EN là đường trung tuyến mà EG = 2/3EN nên G là trọng tâm của∆EDFVậy ∆ABC và ∆EDF có cùng trọng tâm G
Dòng 12 là EN chứ ko pk AN nha, đánh nhầm
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác, gọi I là giao điểm các đường phân giác của tam giác. Chứng minh rằng ba điểm A, G, I thẳng hàng.
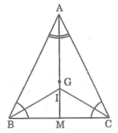
ΔABC cân tại A
⇒ phân giác AI đồng thời là trung tuyến
⇒ AI đi qua trọng tâm G của ΔABC
Vậy A, I, G thẳng hàng.
Đúng 1
Bình luận (0)
Tứ giác ABCD có các đường chéo cắt nhau ở O và không vuông góc với nhau. Gọi H và K lần lượt là trực tâm của các tam giâc AOB và COD gọi G và I lần lượt là trọng tâm của các tam giác BOC và AOD. a Gọi E là trọng tâm của tam giác AOB, F là giao điểm của AH và DK. Chứng minh rằng các tam giác IEG và HFK đồng dạng b Chứng minh rằng IG vuông góc với HK
Xem chi tiết
Tứ giác ABCD có các đường chéo cắt nhau ở O và không vuông góc với nhau. Gọi H và K lần lượt là trực tâm của các tam giâc AOB và COD gọi G và I lần lượt là trọng tâm của các tam giác BOC và AOD. a Gọi E là trọng tâm của tam giác AOB, F là giao điểm của AH và DK. Chứng minh rằng các tam giác IEG và HFK đồng dạng b Chứng minh rằng IG vuông góc với HK
Xem chi tiết