Cho hình vẽ : a,Chứng minh a//b
b,Chứng minh PQ vuông góc AB
c,Chứng minh a//c
cho hình vẽ
a) chứng minh aa'//bb''
b) kẻ OH vuông góc aa' tại H. Chứng minh: OH vuông góc bb'
cho hình vẽ
a) chứng minh aa'//bb''
b) kẻ OH vuông góc aa' tại H. Chứng minh: OH vuông góc bb'
giúp mình với
Cho hình vẽ bên biết : A2 + A3 + B1 = 240 độ và A1 = 120 độ
a, Chứng minh rằng a || b
b, Chứng minh rằng a vuông góc b
Cho hình lập phương ABCD.A'B'C'D' như hình vẽ.
a) Nêu vị trí tương đối của các cặp đường thẳng BC' và A'D'; DD' và AB; AA’ và A’C'.
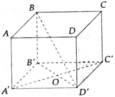
b) Chứng minh A'C' vuông góc với (BB'D'). Từ đó chứng minh A'C' vuông góc BD'.
c) Chứng minh B O = B B ' + 1 4 B ' A ' 2 + B ' C ' 2
Cho hình vẽ . Biết ^M1 = 100 độ , a vuông góc với c , b vuông góc với c
a, Chứng minh a//b
b, Tính các góc ở đỉnh N
a, Vì a và b cùng vuông góc với c nên a//b
a)
Ta có:
\(\begin{cases} a┷c\\ b┷c \end{cases} \)
=> a//b
b) mk ko biết hình thế nào nên ko tính dc nha, thông cảm
cho hình vẽ a vuông góc với c, b vuông góc với c, góc aMP=35 độ và PNb=73 độ
a. chứng minh a // b
b. tính số đo góc MNP
cho hình thang MNPQ ( MN//PQ, MN<PQ ). Gọi A, B, C, D theo thứ tự là trung điểm của MN, MP, PQ, NQ.
a) chứng minh ABCD là hình bình hành
b) biết MNPQ là hình thang cân. chứng minh AC vuông góc với BD
c) hình thang MNPQ phải có thêm điều kiện gì để ABCD là hình vuông? vẽ hình minh họa
Cho tam giác ABC vuông tại A (AB<AC); M là trung điểm của BC. Vẽ MD vuông góc với AB tại D; ME vuông góc với AC tại E.
a) Chứng minh tứ giác ADME là hình chữ nhật.
b) Chứng minh CMDE là hình bình hành.
c) Vẽ AH vuông góc với BC. Chứng minh tứ giác MHDE là hình thang cân
d) Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.
Giúp mình với ạ:<
Cho tam giác abc vuông tại a, trung tuyến am, vẽ me vuông góc ab và mf vuông góc ac.
a, So sánh am và ef
b,Chứng minh emcf là hình bình hành
c, Gọi k là điểm đối xứng của m qua e. Chứng minh akbm là hình thoi
d, Em cắt bf cắt nhau tại p, am và ef cắt nhau tại q. Chứng minh pq song song ab
a) AEMF là hcn (3 góc vuông) nên AM=EF
b) Theo định lí tam giác vuông về đường trung tuyến ứng với cạnh huyền có MA=MB=MC=1/2BC
do đó EF=MC ( cùng bằng AM)
Theo định lí đường trung bình tam giác có ME=FA=FC=1/2AC
nên EFCM là hbh (các cạnh đối bằng nhau)
c) Theo tính đối xứng trục có AM=AK và BM=BK
Mà MA=MB (cmt) nên MA=MB=BK=KA nên AMBK là hthoi (dhnb)
d) CMtt câu a) có EFMB là hbh nên EM và BF cắt nhau tại trung điểm P của mỗi đường
AFEM là hcn nên AM và EF cắt nahu tại trung điểm Q của mỗi đường
Do đó PQ là đường trung bình của tam giác FEB nên PQ//EB hay PQ//AB
Bạn ơi cho mình hỏi chỗ ambk là hình thoi ( là gì vậy bạn )
Cho tam giác ABC cân tại A. Vẽ AH vuông góc BC. a) Chứng minh tam giác AHB=tam giác AHC b) Vẽ HM vuông góc AB, HN vuông góc AC, chứng minh tam giác AMN cân c) Chứng minh MN song song với BC d) Chứng minh AH ^2 + BM^2=AN^2 +BH^2
Vẽ hộ em hình nwuax ạ
a, Xét tam giác AHB và tam giác AHC có
AH _ chung
AB = AC
Vậy tam giác AHB~ tam giác AHC (ch-cgv)
Ta có tam giác ABC cân tại A, có AH là đường cao
đồng thười là đường pg
b, Xét tam giác AMH và tam giác NAH có
HA _ chung
^MAH = ^NAH
Vậy tam giác AMH = tam giác NAH (ch-gn)
=> AM = AN ( 2 cạnh tương ứng )
c, Ta có AM/AB = AN/AC => MN // BC
d, Ta có \(AH^2+BM^2=AN^2+BH^2\)
Xét tam giác BMH vuông tại M \(MB^2=BH^2-MH^2\)
Thay vào ta được \(AH^2+BH^2-MH^2=AN^2+BH^2\Leftrightarrow AH^2-MH^2=AN^2\)
Lại có AM = AN (cmt)
\(AM^2=AH^2-MH^2\)( luôn đúng trong tam giác AMH vuông tại M)
Vậy ta có đpcm