c: \(x^4+x^3-4x^2+x+1\)

\(=x^4-x^3+2x^3-2x^2-2x^2+2x-x+1\)

\(=\left(x-1\right)\left(x^3+2x^2-2x-1\right)\)

\(=\left(x-1\right)\left[\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\right]\)

\(=\left(x-1\right)^2\cdot\left(x^2+3x+1\right)\)

\(x^4+6x^3+11x^2+6x+1\)

\(=x^4+3x^3+x^2+3x^3+9x^2+3x+x^2+3x+1\)

\(=\left(x^2+3x+1\right)^2\)

\(f\left(x\right)=x^4+6x^3+11x^2+6x=x\left(x+1\right)\left(x+2\right)\left(x+3\right)\) 

\(x\) là số nguyên nên \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)\) là tích của \(4\) số nguyên liên tiếp nên trong đó có nhất một số chia hết cho \(4\), một số chia hết cho \(3\), một số chia hết cho \(2\) nhưng không chia hết cho \(4\) nên \(f\left(x\right)\) chia hết cho \(2.3.4=24\). 

Để \(f\left(x\right)\) chia hết cho \(5\) thì \(x,x+1,x+2,x+3\) có một số chia hết cho \(5\). 

Có \(72=2.4.9\) nên để \(f\left(x\right)\) chia hết cho \(72\) thì trong \(4\) số \(x,x+1,x+2,x+3\) có một số chia hết cho \(9\) hoặc hai số chia hết cho \(3\), suy ra \(x\) chia hết cho \(3\). 

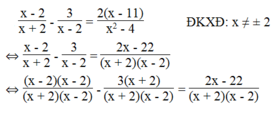
⇔ (x – 2)(x – 2) – 3(x + 2) = 2x – 22

⇔ x 2  – 2x – 2x + 4 – 3x – 6 = 2x – 22

⇔  x 2  – 2x – 2x – 3x – 2x + 4 – 6 + 22 = 0

⇔  x 2  – 9x + 20 = 0

⇔  x 2  – 5x – 4x + 20 = 0

⇔ x(x – 5) – 4(x – 5) = 0

⇔ (x – 4)(x – 5) = 0

⇔ x – 4 = 0 hoặc x – 5 = 0

x – 4 = 0 ⇔ x = 4

x – 5 = 0 ⇔ x = 5

Vậy phương trình có nghiệm x = 4 hoặc x = 5.

5/2\(\times\)1=\(\frac{5}{2\times1}hay=\frac{5}{2}\times1\)

a: \(P\left(x\right)=6x^3+4x^2+2x-4\)

\(Q\left(x\right)=-x^4+6x^3-4x^2+3x-8\)

b: \(P\left(x\right)-Q\left(x\right)=x^4+8x^2-x+4\)

\(P\left(x\right)+Q\left(x\right)=-x^4+12x^3+5x-12\)

a) \(x^2-x+x=4\)

\(x^2=4\)

\(x=\pm2\)

b) \(3x\left(x-5\right)-2\left(x-5\right)=0\)

\(\left(x-5\right)\left(3x-2\right)=0\)

\(\left[{}\begin{matrix}x=5\\x=\dfrac{2}{3}\end{matrix}\right.\)

c) Ta có: \(a+b+c=5-3-2=0\)

\(\left[{}\begin{matrix}x=1\\x=\dfrac{c}{a}=\dfrac{-2}{5}\end{matrix}\right.\)

d) Đặt \(x^2=t\left(t\ge0\right)\) . Lúc đó phương trình trở thành :

\(t^2-11t+18=0\)

\(\left[{}\begin{matrix}t=9\left(tmđk\right)\\t=2\left(tmđk\right)\end{matrix}\right.\)

\(t=9\rightarrow x^2=9\rightarrow x=\pm3\)

\(t=2\rightarrow x^2=2\rightarrow x=\pm\sqrt{2}\)

i) x³- 11x² + 30x

=\(x\left(x^2-11x+30\right)\)

=\(x\left(x-6\right)\left(x-5\right)\)

j) 4x⁴- 21x²y² + y⁴

=4x^4+4x^2y^2+y^4-25x^2y^2

=(2x^2+y^2)^2-(5xy)^2

=(2x^2+y^2-5xy)(2x^2+y^2+5xy)

              k,x³ + 4x²- 7x - 10