Cho tam giác abc vuông tại A đường cao AH, có HB= 9cm, HC=16cm. tính góc B,C
Những câu hỏi liên quan
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. Biết HB=16cm, HC=9cm
a) Tính diện tích tam giác ABC
b) Tính tỉ số lượng giác của góc B
c) Tính số đo góc C
Cho tam giác abc vuông tại a. Đường cao ah
a/ cmr: ah^2 = hb. Hc
B. Biết bh=9cm, hc=16cm
Tính các cạnh của tam giác abc
a) Xét \(\Delta HAC\)và \(\Delta HBA\) có:
\(\widehat{AHC}=\widehat{BHA}=90^0\)
\(\widehat{HAC}=\widehat{HBA}\) cùng phụ với \(\widehat{HAB}\)
suy ra: \(\Delta HAC~\Delta HBA\)
\(\Rightarrow\)\(\frac{AH}{HB}=\frac{HC}{AH}\)
\(\Rightarrow\)\(AH^2=HB.HC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, kẻ đường cao AH (H thuộc cạnh BC). Biết HB = 9cm, HC = 16cm. Tính độ dài: AH, AB.
Cho tam giác ABC vuông tại A, đường cao AH, HB=9cm; HC=16cm. a) chứng minh : AB^2 = HB.BC b) Tính AB; AC; AH c) Phân giác của góc B cắt AH tại I, từ I kẻ đường thẳng song song với BC cắt AC tại K. Chứng minh AK/KC = AB/HC d) Gọi E là giao điểm của BI với AC chứng minh tam giác KIE đồng dạng với tam giác ABI
a: Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC
b: \(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
=>AC=20(cm)
Đúng 0
Bình luận (0)
cho tam giác abc có ah vuông góc bc tại h . có hb=9cm ,hc=16cm ,
Tính ab ,ac,bc
Áp dụng hệ thức lượng giác vào tam giác vuông ABC có:
(AH vuông góc với BC): \(\Rightarrow AH^2=BH\cdot CH=9\cdot16=144\Rightarrow AH=12cm\)
\(\Rightarrow BC=BH+CH=9+16=25cm\)
Áp dụng định lí Pytago vào các tam giác vuông có:
Tam giác vuông \(AHB\) có: \(AB^2=AH^2+BH^2=12^2+9^2=225\Rightarrow AB=15cm\)
Tam giác vuông AHC có: \(AC^2=AH^2+CH^2=16^2+12^2=400\Rightarrow AC=20cm\)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A. Phân giác AD(d thuộc BC), đường cao AH, biết BD=9cm và CD=16cm.
a)tính tỉ số HB/HC
b)tính AH
Cho tam giác ABC vuông ở A. Đường cao AH
a/ AH2=HB=HC
b/ Biết BH=9cm, HC=16cm. Tính các cạnh của tam giác ABC
a, HA^2=HB.HC
Xet tg AHB va tg AHC
Có: H chung
Va góc HCA= góc ABH ( phụ với Â)
=>Tam giác AHB đồng dạng tam giác AHC
=> AH/BH=HC/AH
=>đpcm
b, Ta có: AH/BH=HC/AH
=>AH^2=BH.HC
=>AH^2=144
=>AH=12
*Tính AC
Áp dụng định lý Pi-ta-go:
AC^2=AH^2+HC^2
AC^2=144+256
AC=20cm
*Tính AB
Áp dụng định lý Pi-ta-go:
AB^2=BH^2+AH^2
AB^2=81+144
AB^2=225
AB=15cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có đường cao AH. Cho biết AH= 6cm và HC–HB= 9cm. Tính HB; HC
Ta có: HC - HB = 9 \(\Rightarrow\)HC = HB + 9
Theo hệ thức lượng 2 trong tam giác vuông; ta có:
\(AH^2=BH\times CH=BH\times\left(BH+9\right)\)
\(\Leftrightarrow6^2=BH^2+9BH\)
\(\Leftrightarrow BH^2+9BH-36=0\)
\(\Leftrightarrow BH^2-3BH+12BH-36=0\)
\(\Leftrightarrow\left(BH-3\right)\left(BH+12\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}BH=3\left(tm\right)\\BH=-12\end{cases}}\)
\(\Rightarrow CH=9+BH=9+3=12\)
Vậy BH = 3cm; CH = 12 cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH = 24cm , HB = 16cm.
a ) Tính HC,AB,AC,BC
b ) Tính các góc B,C .
a ) Ta có : \(AH^2=BH.HC\)
\(\Rightarrow HC=\frac{AH^2}{BH}=\frac{24^2}{16}=36\left(cm\right)\)
Ta có : \(BC=BH+HC=16+36=52\left(cm\right)\)
\(\Rightarrow AB^2=BC.BH\)
\(AB^2=52.16\)
\(AB=\sqrt{52.16}\)
\(AB=\sqrt{52}.4\)
\(AB=28,8\left(cm\right)\)
\(\Rightarrow AC^2=BC.HC\)
\(AC^2=52.36\)
\(AC=\sqrt{52.36}\)
\(AC=\sqrt{52}.6\)
\(AC=43,3\left(cm\right)\)
b ) Ta có : \(sin\) \(B=\frac{AC}{BC}=\frac{43,3}{52}=0,83\)
\(\Rightarrow\widehat{B}=56^0\)
\(\Rightarrow\widehat{C}=\widehat{A}-\widehat{B}=90^0-56^0=34^0\).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Biết HB = 9cm; HC = 16cm. Tính AH.
Help me
Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng hệ thức : AH^2 = HB . HC = 16 . 9
=> AH = 4 . 3 = 12 cm
Đúng 3
Bình luận (0)
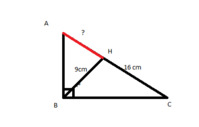
Áp dụng hệ thức liên quan tới đường cao vào Δvuông ABC, ta được:
AH²= BH.CH = 9.16 = 144
⇒ AH=12 (cm)
Đúng 2
Bình luận (0)