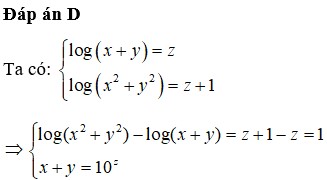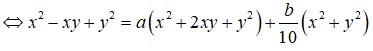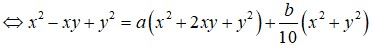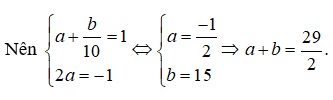Tìm các số nguyên dương x, y, z thỏa mãn x2 + y3 + z4 = 90

Những câu hỏi liên quan
Tìm các số nguyên dương x,y,z thỏa mãn x^2 + y^3 + z^4 = 90
Vì x, y, z là các số nguyên dương nên x,y,z \(\ge1\)
Ta có
\(x^2+y^3+z^4=90\)
\(\Rightarrow z^4< 90\)
Ta thấy rằng \(\hept{\begin{cases}4^4=256>90\\3^4=81< 90\end{cases}}\)nên z không thể lớn hơn 4 được
Hay z nhận các giá trị là 1, 2, 3
Với z = 3 thì
\(x^2+y^3=90-3^4=9\)
Tương tự như trên ta cũng thấy được: y chỉ thể nhận các giá trị 1,2
Thế vô lần lược tìm được: y = 2, x = 1
Xét lần lược các trường hợp của z sẽ tìm được các nghiêm còn lại
Các bộ số cần tìm là: \(\left(x,y,z\right)=\left(1,2,3\right);\left(5,4,1\right);\left(9,2,1\right)\)
Mình chỉ hướng dẫn bạn cách làm thôi nhé.
Đúng 0
Bình luận (0)
Vì x,y,z là các số nguyên dg nên x,y,z >/1
Ta có : x2 +y3 +z4 = 90
Suy ra z4 < 90
Ta thấy rằng {42 = 256 > 90 , 34 = 81 < 90 nên z ko thể >4
Hay z nhận các gt là 1,2,3
Với z=3 thì :
x2
Tìm các số nguyên dương x,y,z thỏa mãn x^2+y^3+z^4=90.
Tìm các số nguyên dương thỏa mãn x3 - y3 = 133(x2 + y2)
Tìm các số nguyên dương x , y , z thỏa mãn x2 + y3 + z4 = 90
Bạn tham khảo ở đây nhé
Câu hỏi của Nguyễn Quang Đức - Toán lớp 6 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Giả sử a,b là các số thực sao cho
x
3
+
y
3
a
10
3
x
+
b
10
2
x
đúng với mọi các số thực dương x, y, z thỏa mãn
log
(
x
+
y...
Đọc tiếp
Giả sử a,b là các số thực sao cho x 3 + y 3 = a 10 3 x + b 10 2 x đúng với mọi các số thực dương x, y, z thỏa mãn log ( x + y ) = z và log ( x 2 + y 2 ) = z + 1 . Giá trị của a+b bằng
A. -31/2
B. -25/2
C. 31/2
D. 29/2
tìm các số x ,y, z biết (-x2.y3)2+(2.y2.z4)3=0
Lời giải:
Ta thấy:
$(-x^2y^3)^2\geq 0$ với mọi $x,y$
$(2y^2z^4=2(yz^2)^2\geq 0$ với mọi $y,z$
$\Rightarrow (2y^2z^4)^3\geq 0$ với mọi $y,z$
Do đó để tổng $(-x^2y^3)^2+(2y^2z^4)^3=0$ thì:
$-x^2y^3=2y^2z^4=0$
Hay $(x,y,z)=(x,0,z)$ với $x,z$ bất kỳ hoặc $(x,y,z)=(0,y,0)$ với $y$ là số bất kỳ.
Đúng 0
Bình luận (0)
Giả sử a, b là các số thực sao cho x3 + y3 a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) z và log(x2 + y2) z + 1. Giá trị của a+b bằng: A.
-
31
2
B.
-
25
2
C.
31
2
D.
29
2
Đọc tiếp
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Đáp án D.
Ta có
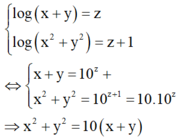
Khi đó
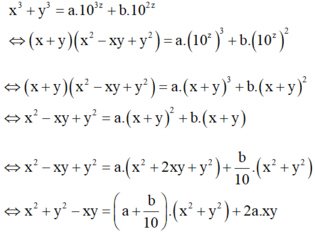
Đồng nhất hệ số, ta được

Đúng 0
Bình luận (0)
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2