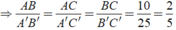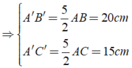cho ABC, AB+AC=16 cm, A= 90 độ. Tìm các cạnh của tam giác ABC để SABC lớn nhất

Những câu hỏi liên quan
tam giác abc có góc a<90 trên cạnh ab lấy d trên cạnh ac lấy e gọi diện tích tam abc là Sabc diện tích tam ade là Sade a ,chứng minh Sade/Sabc =ad.ae/ab.ac b, cho de //bc xác định vị trí của d để diện tích tam giác bde lớn nhất
dễ thấy Sabc =\(\frac{1}{2}\) AB.AC.sinA; Sade= \(\frac{1}{2}\)AD.AE.sinA
=> Sabc/Sade=ad.ae/ab.ac
de//bc thì \(\frac{AD}{AB}=\frac{DE}{BC}=>\frac{BD}{AB}=\frac{BC-DE}{BC}=>BD=\frac{AB\left(BC-DE\right)}{BC}\)
SBDE = \(\frac{1}{2}BD.DEsin\widehat{BDE}=\frac{1}{2}\frac{AB\left(BC-DE\right)}{BC}.DE.cos\widehat{ABC}=\)\(\frac{AB.cos\widehat{ABC}}{2BC}\left(BC.DE-DE^2\right)\)
BC.DE - DE2 = \(\frac{BC^2}{4}-\)(\(\frac{BC}{2}-DE\))2 \(\le\frac{BC^2}{4}\)
vậy SBDE đạt GTLN khi DE= \(\frac{BC}{2}\)hay \(\frac{DE}{BC}=\frac{1}{2}=\frac{AD}{AB}\) hay D là trung điểm AB
Help!!!!!
Cho tam giác abc có góc A<90 độ. Lấy D thuộc AB, lấy E thuộc AC.
a) Chứng minh Sade/Sabc=AD.AE/AB.AC(xong)
b)cho DE//BC. Tìm vị trí của D để Sbde lớn nhất
cho tam giác abc có góc a = 60 độ góc c < góc B < 90 độ
a, cm ab<ac
b cm trên cạnh ac lấy điểm m sao cho am = ab .Chứng minh tam giác abm là tam giác đều
c, so sánh các cạnh của tam giác abc
a: góc C<góc B
=>AB<AC
b: Xét ΔABM co AB=AM và góc A=60 độ
nên ΔAMB đều
Đúng 0
Bình luận (0)
Cho Δ ABC có AB = 8cm, AC = 6cm, BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?
A. 4cm; 3cm
B. 7,5cm; 10cm
C. 4,5cm; 6cm
D. 15cm; 20cm
Cho Δ ABC có AB = 8cm,AC = 6cm,BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?
A. 4cm; 3cm
B. 7,5cm; 10cm
C. 4,5cm; 6cm
D. 15cm; 20cm
Ta có: Δ ABC đồng dạng Δ A'B'C'
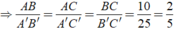
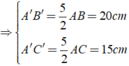
Chọn đáp án D.
Đúng 0
Bình luận (0)
1.Cho tam giác ABC ,A90.Biết AB+AC49cm,AB-AC7cm.Tính cạnh BC .2.Cho tam giác cân ABC, ABAC17cm.Kẻ BDvuôngAC.Tính cạnh đáy BC, biết BD15cm.3. Tính cạnh đáy BC của tam giác cân ABC, biết rằng đường vuông góc BH kẻ từ B xuống cạnh AC chia AC thành 2 phần:AH8cm,HC3cm.4. Một tam giác vuông có cạnh huyền là 102 cm, các cạnh góc vuông tỉ lệ với 8:5. Tính các cạnh của tam giác vuông đó.5. Cho tam giác ABC, biết BC bằng 52cm, AB 20cm ,AC48 cm.a, Chứng minh tam giác ABC vuông ở A;b, Kẻ AH vuông góc với...
Đọc tiếp
1.Cho tam giác ABC ,A=90.Biết AB+AC=49cm,AB-AC=7cm.Tính cạnh BC .
2.Cho tam giác cân ABC, AB=AC=17cm.Kẻ BDvuôngAC.Tính cạnh đáy BC, biết BD=15cm.
3. Tính cạnh đáy BC của tam giác cân ABC, biết rằng đường vuông góc BH kẻ từ B xuống cạnh AC chia AC thành 2 phần:AH=8cm,HC=3cm.
4. Một tam giác vuông có cạnh huyền là 102 cm, các cạnh góc vuông tỉ lệ với 8:5. Tính các cạnh của tam giác vuông đó.
5. Cho tam giác ABC, biết BC bằng 52cm, AB = 20cm ,AC=48 cm.
a, Chứng minh tam giác ABC vuông ở A;
b, Kẻ AH vuông góc với BC. Tính AH .
6. Cho tam giác vuông cân ABC, A=90.Qua A kẻ đường thẳng d tùy ý. Từ B và C kẻ BH vuông d. Chứng minh rằng tổng BH^2+CK^2 ko phụ thuộc vào vị trí của đường thẳng d.
7. Cho tam giác vuông ABC ,A= 90 độ. Trên nửa mặt phẳng bờ AC không chứa điểm B, kẻ tia CX sao cho CA là tia phân giác của gócBCx.Từ A kẻ AE vuông Có, từ B kẻ BD vuông AE. Gọi AH là đường cao của tam giác ABC. Chứng minh rằng :
a, A là trung điểm của DE
b, DHE=90 độ
8. Cho tam giác ABC có A bằng 90 độ,AB=8 cm,BC =17cm.Trên nửa mặt phẳng bờ AC ko chứa điểm B, vẽ tia CD vuông với AC và CD=36cm.Tính tổng độ dài các đoạn thẳngAB+BC+CD+DA.
Bài 1:
Độ dài cạnh AB: ( 49 + 7 ) : 2 = 28 (cm)
Độ dài cạnh AC: 28 - 7 = 21 (cm)
Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:
\(BC^2=AC^2+AB^2\)
Hay \(BC^2=21^2+28^2\)
\(\Rightarrow BC^2=441+784\)
\(\Rightarrow BC^2=1225\)
\(\Rightarrow BC=35\left(cm\right)\)
Đúng 0
Bình luận (0)
Bài 2:
Áp dụng định lý Py-ta-go vào tam giác ABD vuông tại D có:
\(AB^2=AD^2+BD^2\)
\(\Rightarrow AD^2=AB^2-BD^2\)
Hay \(AD^2=17^2-15^2\)
\(\Rightarrow AD^2=289-225\)
\(\Rightarrow AD^2=64\)
\(\Rightarrow AD=8\left(cm\right)\)
Trong tam giác ABC có:
\(AD+DC=AC\)
\(\Rightarrow DC=AC-AD=17-8=9\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác BCD vuông tại D có:
\(BC^2=BD^2+DC^2\)
Hay \(BC^2=15^2+9^2\)
\(\Rightarrow BC^2=225+81\)
\(\Rightarrow BC^2=306\)
\(\Rightarrow BC=\sqrt{306}\approx17,5\left(cm\right)\)
Đúng 0
Bình luận (0)
Bài 3:
Vì tam giác ABC cân tại A (gt) nên AB = AC
Mà AC = AH + HC
Hay AC= 8 + 3 = 11 (cm)
Nên AB = 11 (cm)
..........
( Phần này áp dụng định lý Py-ta-go vào tam giác và làm giống như bài 2 vậy nên mình không giải lại nữa nha bạn ) ( ^ o ^ )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC,góc A bằng 90 độ, AB=24 cm, AC=18 cm. Từ trung điểm M trên cạnh BC, kẻ đường vuông góc với BC, cắt AC tại D, AB tại E. a) Chứng minh DMC đồng dạng ABC và tính độ dài các cạnh của tam giác DMC ? b) Tính BE ?
a: Xét ΔDMC vuông tại M và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔDMC\(\sim\)ΔABC
Đúng 0
Bình luận (0)
CHO TAM GIÁC VUÔNG ABC ( GÓC A = 90 ĐỘ) , ĐƯỜNG CAO AH.
BIẾT AB: AC=1:\(\sqrt{3}\) VÀ HC-HB=8CM.
A.TÍNH CÁC CẠNH CỦA TAM GIÁC ABC
B. HÌNH CHỮ NHẬT MNPQ NỘI TIẾP TAM GIÁC ABC( CÁC ĐIỂM P VÀ Q THUỘC CẠNH BC ; M THUỘC CẠNH AB VÀ N THUỘC CẠNH AC). TÌM GIÁ TRỊ LỚN NHẤT CỦA DIỆN TÍCH HÌNH CHỮ NHẬT MNPQ.
Cho tam giác ABC có độ dài các cạnh A B = 4 c m , A C = 5 c m , B C = 5 c m . Tìm góc lớn nhất của tam giác
A. Góc A
B. Góc B
C. Góc C
D. Góc B và góc A
Vì cạnh AC = BC = 5cm nên ∠B = ∠A và cùng là góc lớn nhất. Chọn D
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH.
a) Chứng minh : tam giác ABC đồng dạng với tam giác HAC.
b) Biết AB = 6 cm , AC = 8 cm.Tính độ dài các cạnh BC , AH, CH , BH.
c) Trên AH lấy điểm M sao cho AM= 1,2 cm , từ điểm M kẻ đường thẳng song song với BC lần lượt cagws AB và AC tại E và F. Tính Saef phần Sabc, Sabc , Saef.
a) Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat{BAC}=\widehat{AHC}=90^0\)
\(\widehat{ABC}=\widehat{HAC}\) do cùng phụ với góc BAH )
suy ra: \(\Delta ABC~\Delta HAC\)
b) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
Áp dụng hệ thức lượng ta có:
\(AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8\)cm
\(CH=\frac{AC^2}{BC}=\frac{8^2}{10}=6,4\)cm
\(BH=BC-HC=10-6,4=3,6\)cm
Đúng 1
Bình luận (0)