bó tay . com . vn

e: =>x(x^3-4x^2-8x+8)=0

=>x[(x^3+8)-4x(x+2)]=0

=>x(x+2)(x^2-2x+4-4x)=0

=>x(x+2)(x^2-6x+4)=0

=>\(x\in\left\{0;-2;3+\sqrt{5};3-\sqrt{5}\right\}\)

g: =>2x^4+5x^3-6x^3-15x^2+6x^2+15x-2x-5=0

=>(2x+5)(x^3-3x^2+3x-1)=0

=>(2x+5)(x-1)^3=0

=>x=1 hoặc x=-5/2

h: =>(x^2+8x+7)(x^2+8x+15)+15=0

=>(x^2+8x)^2+22(x^2+8x)+120=0

=>(x^2+8x+10)(x^2+8x+12)=0

=>(x^2+8x+10)(x+2)(x+6)=0

=>\(x\in\left\{-2;-6;-4+\sqrt{6};-4-\sqrt{6}\right\}\)

Ta sử dụng phương pháp chia đa thức bằng phép chia đa thức tổng quát để giải bài toán này. Theo đó, ta có:
2x^4 + 4x³-3x² - 4x + 1: (x² - 1)
= 2x² + 4x + 1 - (x² + 4x + 1)/(x² - 1)
= 2x² + 4x + 1 - (x² - 1 + 4x+2)/(x² -
1)
= 2x² + 4x + 1 - (x² + 4x + 2)/(x² - 1) +
1/(x² - 1) = 2x² + 4x + 1 - (x² + 4x + 2)/(x² - 1) +
1/[(x+1)(x-1)]
Vậy kết quả là:
A(x) (x²-1)=2x² + 4x + 1 - (x² + 4x +
2)/(x² - 1) + 1/[(x+1)(x-1)]

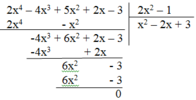
Vậy (2x4 – 4x3 + 5x2 + 2x – 3) : (2x2 – 1) = x2 – 2x + 3.

\(P\left(x\right)=2x^2+1\)

\(\dfrac{1.4+2.6+3.8+4.10+5.12}{5.2+10.3+15.4+20.5+25.6}\)

\(=\dfrac{2\left(1.2+2.3+3.4+4.5+5.6\right)}{5\left(1.2+2.3+3.4+4.5+5.6\right)}\)

\(=\dfrac{2}{5}\)

Ta có: f(x) + g(x) – h(x)

      = (x5 – 4x3 + x2 – 2x + 1) + (x5 – 2x4 + x2 – 5x + 3) – (x4 – 3x2 + 2x – 5)

      = x5 – 4x3 + x2 – 2x + 1 + x5 – 2x4 + x2 – 5x + 3 – x4 + 3x2 - 2x + 5

      = (x5 +x5) – (2x4 + x4) – 4x3 + (x2 + x2 + 3x2)- (2x + 5x + 2x) + (1 + 3 + 5)

      = (1 + 1)x5 – (2 + 1)x4 – 4x3 + (1 + 1 + 3)x2 - (2 + 5 + 2)x + (1 + 3 + 5)

      = 2x5 – 3x4 – 4x3 + 5x2 – 9x + 9

a) \(P\left(x\right)=3x^3-x^2-2x^4+3+2x^3+x+3x^4-x^2-2x^4+3+2x^3+x+3x^4\)

 \(=2x^4+7x^3-2x^2+2x+6\)

\(Q\left(x\right)=-x^4+x^2-4x^3-2+2x^2-x-x^3-x^4+x^2-4x^3-2+2x^2-x-x^3\)

\(=-2x^4-10x^3+6x^2-2x-4\)

b) \(P\left(x\right)+Q\left(x\right)=2x^4+7x^3-2x^2+2x+6-2x^4-10x^3+6x^2-2x-4\)

                                      \(=-3x^3+4x^2+2\)