Cho x, y thay đổi thỏa mãn x+y=1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức:
\(B=\left(4x^2+3y\right)\left(4y^2+3x\right)+25xy\)

Những câu hỏi liên quan
Cho các số dương x,y thỏa mãn \(x+y=1\)
Tìm giá trị lớn nhất của biểu thức \(Q=\left(4x^2+3y\right)\left(4y^2+3x\right)+25xy\)
Thái đức anh Ơ CTV là không được hỏi bài à ??? Bài này tôi làm ra lâu rồi,đăng lên chơi vui thôi nhé ! Không làm thì đừng có mà spam lung tung câu hỏi của tôi
Vài bước nhân tung ..v.v là ra ấy mà:v
\(Q=16x^2y^2+12\left(x^3+y^3\right)+9xy+25xy\)
\(=\frac{\left(8xy+1\right)\left(4xy-1\right)}{2}+\frac{25}{2}+12\left(x+y-1\right)\left(x^2-xy+y^2+x+y+1\right)\le\frac{25}{2}\)
Đẳng thức xảy ra khi \(x=y=\frac{1}{2}\).
Max là 25/2 khi ...
Xem thêm câu trả lời
Cho các số thực không âm x, y thay đổi và thỏa mãn x + y = 1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S = (4x2 + 3y)(4y2 + 3x) + 25xy.
Cho hai số x,y thay đổi và thỏa mãn \(x^2+y^2=1\) . Tìm giá trị lớn nhất và nhỏ nhất của biểu thức \(P\left(x,y\right)=x^2+y^2-4x\)
Từ giả thiết x2 + y2 = 1, suy ra x2 \(\le\)1 => -1 \(\le x\le\)1 (1)
Ta có P(x,y) = x2 + y2 - 4x = 1 - 4x (2)
Từ (1), (2) suy ra \(-3=1-4\cdot1\le P\le1-4\cdot\left(-1\right)=5\)
Vậy Max P = 5, Min P = -3.
Đúng 0
Bình luận (0)
Quang Cảm ơn bạn !
Có ai có cách giải khác không nhỉ?
Đúng 0
Bình luận (0)
a) 9x2 - 36
=(3x)2-62
=(3x-6)(3x+6)
=4(x-3)(x+3)
b) 2x3y-4x2y2+2xy3
=2xy(x2-2xy+y2)
=2xy(x-y)2
c) ab - b2-a+b
=ab-a-b2+b
=(ab-a)-(b2-b)
=a(b-1)-b(b-1)
=(b-1)(a-b)
P/s đùng để ý đến câu trả lời của mình
Đúng 0
Bình luận (0)
cho 2 số thực x,y thỏa mãn điều kiên \(x+y+25=8\left(\sqrt{x-1}+\sqrt{y-5}\right)\). Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: \(P=\sqrt{\left(x-1\right)\left(y-5\right)}\)
Cho các số thực dương x;y thỏa mãn: \(6x+9-\sqrt{y}.\left(y+1\right)=3y-\left(2x+4\right).\sqrt{2x+3}\). Tìm giá trị nhỏ nhất của biểu thức: \(D=xy+3y-4x^2-3\)
Tìm giá trị nhỏ nhất của các biểu thức sauAx^2-4x+1 B4x^2+4x+11 Cleft(x-1right)left(x+3right)left(x+2right)left(x+6right)D2x^2+y^2-2xy+2x-4y+9 Tìm giá trị lớn nhất của các biểu thức sauE5-8x-x^2F4x-x^2+1
Đọc tiếp
Tìm giá trị nhỏ nhất của các biểu thức sau
A=\(x^2-4x+1\) \(B=4x^2+4x+11\)
\(C=\left(x-1\right)\left(x+3\right)\left(x+2\right)\left(x+6\right)\)
\(D=2x^2+y^2-2xy+2x-4y+9\)
Tìm giá trị lớn nhất của các biểu thức sau
\(E=5-8x-x^2\)
\(F=4x-x^2+1\)
Cho x,y,z là các số thực dương thỏa mãn đẳng thức xy+yz+zx=5. Tìm giá trị nhỏ nhất của biểu thức
\(P=\frac{3x+3y+3z}{\sqrt{6\left(x^2+5\right)}+\sqrt{6\left(y^2+5\right)}+\sqrt{6\left(z^2+5\right)}}\)
Mình nghĩ phần phân thức là $3x+3y+2z$ thay vì $3x+3y+3z$. Nếu là vậy thì bạn tham khảo lời giải tại link sau:
Cho x, y, z là các số thực dương thỏa mãn đẳng thức xy yz zx=5. Tìm GTNN của biểu thức \(P=\frac{3x 3y 2z}{\sqrt{6\left(... - Hoc24
Đúng 1
Bình luận (2)
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức
S
(
4
x
2
+
3
y
)
(
4
y
2
+
3
x
)
+
25
x
y
là: A.
M
25
2
;
m...
Đọc tiếp
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y=1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức S = ( 4 x 2 + 3 y ) ( 4 y 2 + 3 x ) + 25 x y là:
A. M = 25 2 ; m = 191 16 .
B. M = 12 ; m = 191 16 .
C. M = 25 2 ; m = 12 .
D. M = 25 2 ; m = 0 .
Do x+ y= 1 nên
S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y , d o x + y = 1 = 16 x 2 y 2 - 2 x y + 12
Đặt t= xy . Do x≥ 0 ; y≥0 nên
0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4
Xét hàm số f(t) = 16t2- 2t + 12 trên [0 ; 1/4].
Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16 .
Bảng biến thiên
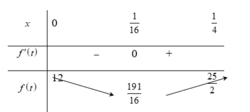
Từ bảng biến thiên ta có:
m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ; m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2
Vậy giá trị lớn nhất của S là 25/2 đạt được khi
x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2
giá trị nhỏ nhất của S là 191/ 16 đạt được khi
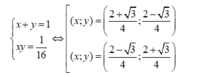
Chọn A.
Đúng 0
Bình luận (0)
Cho x,y là các số thực thỏa mãn:\(\left(x+y\right)^2+7\left(x+y\right)+y^2+10=0\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức :A=x+y+1.
A = x +y +1 => A - 1 = x +y.
Từ gt suy ra : (A -1)2 + 7(A -1) + y2 + 10 = 0 => A2 + 5A + 4 + y2 = 0 => A2 + 5A + 4 = - y2 <= 0. Dấu = xảy ra khi y = 0
=> (A +1)(A +4) <= 0 => - 1 <= A <= -4
A = -1 <=> y = 0 và x + y = -1 => y = 0 và x = -1
A = -4 <=> y =0 và x + y = -4 => y = 0 và x = -4
Vậy minA = -1 khi x = -1, y = 0
maxA = -4 khi x = -4, y = 0
Đúng 0
Bình luận (0)



















