Giúp mình bài rút gọn với ạ

Những câu hỏi liên quan
Giúp mình bài b này với ạ
đề là rút gọn ạ
giải giúp mình với ạ, đây là bài rút gọn biểu thức nha
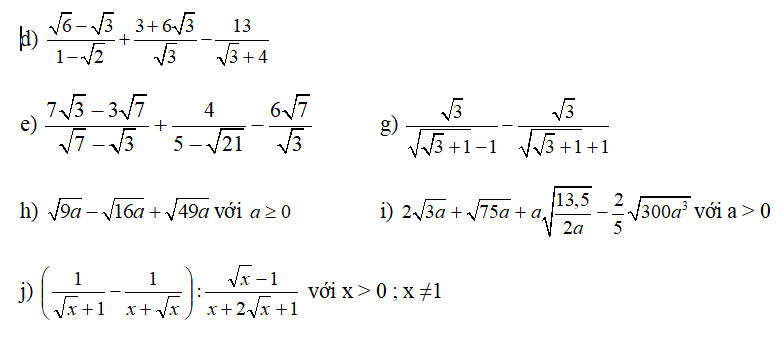
d: \(\dfrac{-\left(\sqrt{3}-\sqrt{6}\right)}{1-\sqrt{2}}+\dfrac{6\sqrt{3}+3}{\sqrt{3}}-\dfrac{13}{4+\sqrt{3}}\)
\(=-\sqrt{3}+6+\sqrt{3}-4+\sqrt{3}\)
\(=2+\sqrt{3}\)
Đúng 0
Bình luận (0)
Giúp mình phần 2) [bài rút gọn] với ạ mình tìm mãi k ra kết quả 😢
\(P=\left(\dfrac{x-1}{\sqrt{x}+1}-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}}+1\right).\dfrac{1}{x\sqrt{x}+1}\)
\(=\left(\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+1}-\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)}+1\right).\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\left(\sqrt{x}-1-\dfrac{\sqrt{x}-1}{\sqrt{x}}+1\right).\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)+\sqrt{x}}{\sqrt{x}}.\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}.\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}=\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
Đúng 2
Bình luận (0)
Bài 2:
Ta có: \(P=\left(\dfrac{x-1}{\sqrt{x}+1}-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}}+1\right)\cdot\dfrac{1}{x\sqrt{x}+1}\)
\(=\left(\sqrt{x}-1-\dfrac{\sqrt{x}-1}{\sqrt{x}}+1\right)\cdot\dfrac{1}{x\sqrt{x}+1}\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{1}{x+\sqrt{x}}\)
Đúng 0
Bình luận (0)
Bài 1: Rút gọn phân số:
a) -315/540 b)25.13/26.35 c)6.9-2.17/63.3-119 d)3.13-13.18/15.40-80 giải giúp mình với ạ mình cần gấp ạ!a, \(-\dfrac{315}{540}\) = \(\dfrac{-315:45}{540:45}\) = \(\dfrac{-7}{12}\) b, \(\dfrac{25.13}{26.35}\) = \(\dfrac{25.13:5:13}{26.35:13:5}\) = \(\dfrac{5}{14}\)
c, \(\dfrac{6.9-2.17}{63.3-119}\) = \(\dfrac{2.3.9-2.17}{7.9.3-7.17}\) = \(\dfrac{2.(27-17)}{7.(7-17)}\) = \(\dfrac{2}{7}\)
d, \(\dfrac{3.13-13.18}{15.40-80}\) = \(\dfrac{3.13(1-6)}{40.(15-2)}\) = \(\dfrac{-3.13.5}{40.13}\) = \(\dfrac{-15}{40}\) = \(\dfrac{-15:5}{40:5}\) = \(-\dfrac{3}{8}\)
Đúng 1
Bình luận (0)
Ai giúp em bài hàm số với bài hình với ạ nếu rảnh giúp em luôn câu c, bài rút gọn ạ;v

Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)
Đúng 1
Bình luận (0)
giúp mình với ạ rút gọn biểu thức ạ
Đọc tiếp
giúp mình với ạ rút gọn biểu thức ạ
\(B=9x^4-\left(2x+1\right)^2-\left(9x^4+6x^2+1\right)\\ =9x^4-4x^2-4x-1-9x^4-6x^2-1\\ =-10x^2-4x-2\)
Đúng 0
Bình luận (1)
\(B=\left(3x^2+1-2x\right)\left(3x^2+1+2x\right)-\left(3x^2+1\right)^2\\ B=\left(3x^2+1\right)^2-4x^2-\left(3x^2+1\right)^2=-4x^2\)
Đúng 2
Bình luận (0)
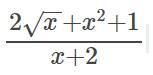 Rút gọn giúp mình với ạ
Rút gọn giúp mình với ạ
ĐKXĐ: \(x\ge0\)
\(\dfrac{2\sqrt{x}+x^2+1}{x+2}=\dfrac{\left(\sqrt{x}+1\right)^2}{x+2}\)
Đúng 0
Bình luận (0)
Giúp mình với cảm ơn trước ạ
Bài 7: rút gọn \(\dfrac{\left(x-1\right)\sqrt{3}}{\sqrt{x^2-x+1}}x=2+\sqrt{3}\)
Giúp em với ạ, bài rút gọn biểu thức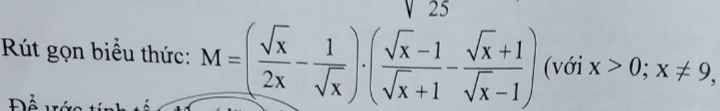
\(M=\left(\dfrac{\sqrt{x}}{2x}-\dfrac{1}{\sqrt{x}}\right)\cdot\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\\ =\left(\dfrac{\sqrt{x}}{2x}-\dfrac{2\sqrt{x}}{2x}\right)\cdot\left(\dfrac{\left(\sqrt{x}-1\right)^2-\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\\ =\dfrac{x-2\sqrt{x}}{2x}\cdot\dfrac{x-2\sqrt{x}+1-\left(x+2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{-4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-2\right)}{x-1}\)
Đúng 1
Bình luận (0)
Giải hộ mình bài này với ạ rút gọn P
ĐKXĐ: x>0; x ≠ 1
P = \(\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+4\sqrt{x}\right)\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\)
= \(\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1+4x\sqrt{x}-4\sqrt{x}}{x-1}.\dfrac{x-1}{\sqrt{x}}\)
= \(\dfrac{4x\sqrt{x}}{\sqrt{x}}\)= 4x
Vậy P = 4x với x > 0; x ≠ 1
Đúng 1
Bình luận (0)























