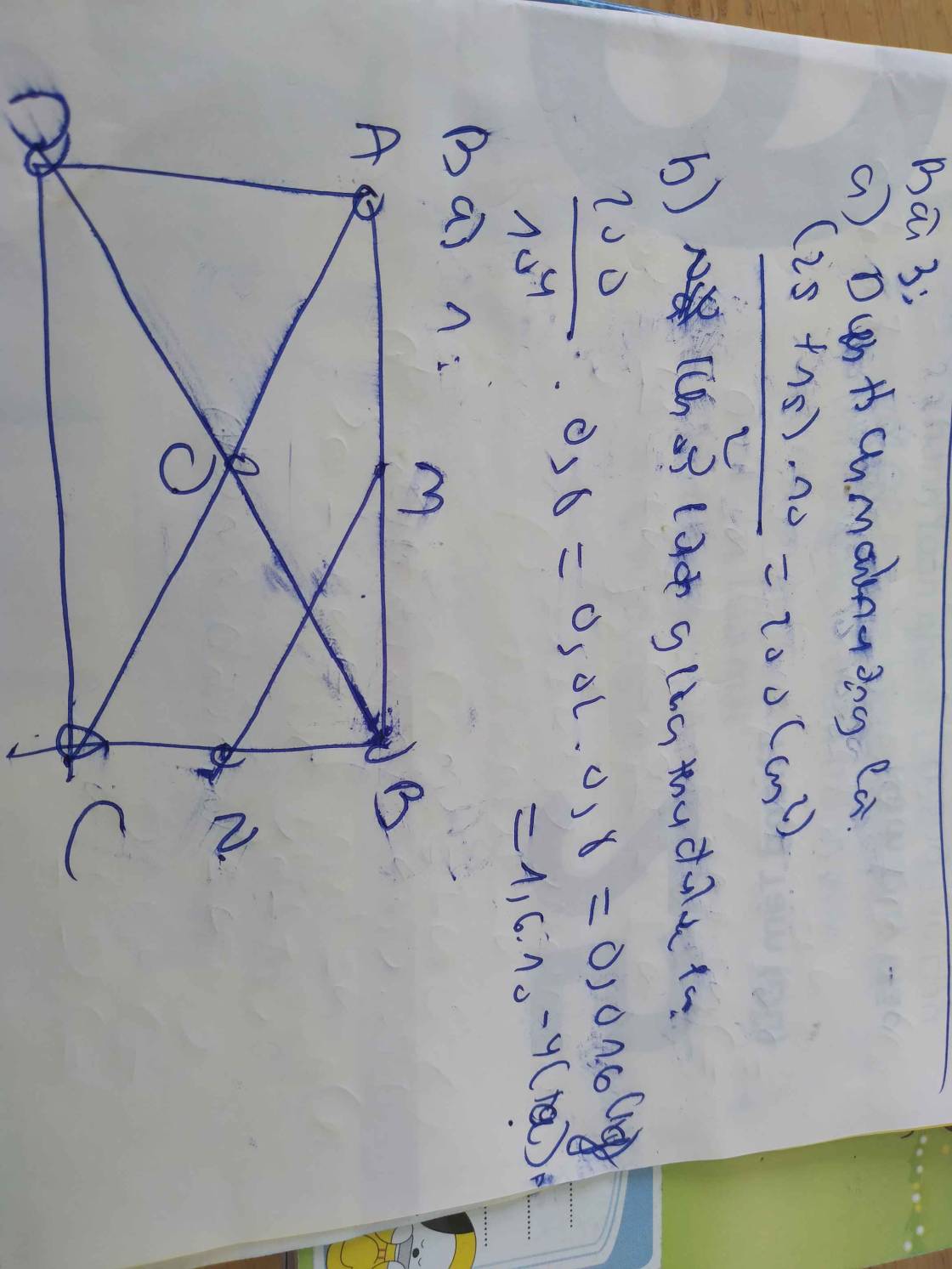
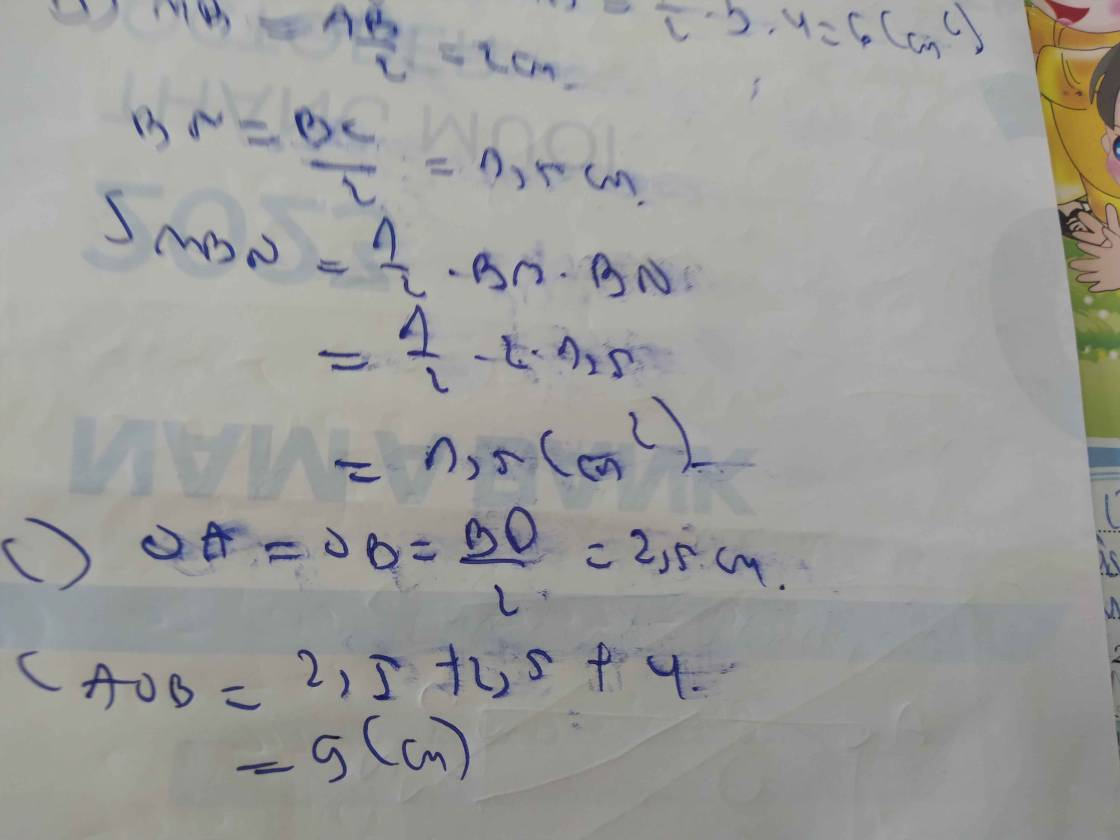Cho hình vuông ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của AB và BC. Gọi H là giao điểm của CM và DN. Tính diện tích tam giác DAH biết a = 20,16 cm.

Những câu hỏi liên quan
Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB và BC. Chứng minh
a) DN = CM, DN vuông góc CM
b) Gọi H là giao điểm của DN và CM, I là trung điểm của CD và Ak là đường cao của tam giác AHD. Chứng minh A, K, I thẳng hàng
Cho hình vuông ABCD có cạnh bằng 4 cm. Gọi M và N lần lượt là trung điểm cạnh AB và BC. Nối MN cắt DN ở E
a) C/m : CM vuông góc với DN
b) Tính chính xác tỉ số lượng giác góc CMN
c) Tính diện tích tam giác MDN
Cho hình vuông ABCD có cạnh bằng 12 cm.
a, Tính diện tích hình vuông ABCD
b,Gọi M , N là trung điểm của AB và BC . I là giao điểm của MC và ND . Tính diện tích tam giác INC
a ) Diện tích hình vuông ABCD là :
12 x 12 = 144 (cm2)
Đúng 1
Bình luận (0)
a diện tích ABCD là
12x12=144[cm2]
Đúng 0
Bình luận (0)
b ) Có : N là trung điểm của BC => NB=NC = \(\frac{1}{2}\)x BC =6 ( cm)
Diện tích hình tam giác INC là :
(6x12):2 = 36
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho hìnhvuông ABCD có cạnh bằng a . Gọi E,F,G,H, lần lượt là trung điểm các cạnh AB ,BC,CD,DA,. M là giao điểm của CE và DF
a) CM : tứ giác EFGH là hình vuông
b)CM: DF vuông góc với CE và tam giacs MAD cân
c)tính diện tích tam giác MADtheo a
Cho hình vuông ABCD có cạnh bằng a. Gọi E;F;G;H lần lượt là trung điểm của các cạnh AB;BC;CD;DA. Gọi M là giao điểm của CE và DF. Tính diện tích tam giác MDC theo a
Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng a. Gọi E,F,G,H lần lượt là trung điểm của cách cạnh AB,BC,CD,DA.M là giao điểm của CE và DF.
a)CM EFGH là hình vuông
b)EC vuông góc vs DF
c)tính diện tích của tam giác MDC theo a (ko dùng đồng dạng)
Bài1,Cho hình chữ nhật ABCD có các cạnh AB bằng 4 cm AD 3 cm đường chéo AC bằng 5 cm A,tính chu vi và diện tích của hình chữ nhật ABCD và tam giác ABDB,Gọi M là trung điểm của AB N là trung điểm của BC.Tính diện tích tam giác MBNC,Gọi O là giao điểm của AC và BD.Tính chu vi tam giác AOB Bài2, 1 khu vườn hình chữ nhật có chiều dài 15m ,chiều rộng 10m,cổng nào có độ rộng 1/3 chiều dài,phần còn lại là hàng rào.Hỏi hàng rào của khu vườn bảo nhiêu mBài3, 1 mảnh ruộng hình thang có đáy lớn25cm đáy bé...
Đọc tiếp
Bài1,Cho hình chữ nhật ABCD có các cạnh AB bằng 4 cm AD = 3 cm đường chéo AC bằng 5 cm A,tính chu vi và diện tích của hình chữ nhật ABCD và tam giác ABD
B,Gọi M là trung điểm của AB N là trung điểm của BC.Tính diện tích tam giác MBN
C,Gọi O là giao điểm của AC và BD.Tính chu vi tam giác AOB Bài2, 1 khu vườn hình chữ nhật có chiều dài 15m ,chiều rộng 10m,cổng nào có độ rộng= 1/3 chiều dài,phần còn lại là hàng rào.Hỏi hàng rào của khu vườn bảo nhiêu m
Bài3, 1 mảnh ruộng hình thang có đáy lớn=25cm đáy bé=15cm,chiều cao=10cm
A,Tính diện tích mảnh ruộng
B,biết 5 suất lúa là 0,8 kg trên m². Hỏi mảnh ruộng cho sản lượng là bao nhiêu tạ thóc. GIÚP EM VỚI Ạ:33:(
cho hình vuông ABCD gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB,BC,CD,DA.gọi E,H lần lượt là giao điểm của AP với BQ và DN; F,G lần lượt là giao điểm của CM với BQ và DN. CMinh AP//CM và góc DAP =góc CDN
Cho hình vuông ABCD có cạnh bằng a. Gọi E;F;G;H lần lượt là trung điểm của các cạnh AB;BC;CD;DA. Gọi M là giao điểm của CE và DF.
a) Chứng minh: EFGH là hình vuông.
b) Chứng minh: DF vuông góc CE và tam giác MAD cân
c) Tính diện tích tam giác MDC theo a